Az A. 912. feladat (2025. szeptember)

A. 912. Egy \(\displaystyle ABC\) háromszög \(\displaystyle A\) csúcsához tartozó szimmedián egyenese a körülírt kört \(\displaystyle A'\)-ben metszi el másodszorra. Mutassuk meg, hogy az alábbi három pont egy egyenesre illeszkedik:

• az \(\displaystyle A\) pont \(\displaystyle BC\) egyenesre vett tükörképe;
• az \(\displaystyle A\) pont inverz képe az \(\displaystyle ABC\) háromszög Feuerbach-körére vett inverzió során;
• az \(\displaystyle AA'\) húr felezőpontja.

Javasolta: Szakács Ábel, Budapest

(7 pont)

A beküldési határidő 2025. október 10-én LEJÁRT.

Vezessünk be néhány jelölést: a \(\displaystyle BC,CA,AB\) oldalak felezőpontjai rendre legyenek \(\displaystyle D,E,F\), jelölje \(\displaystyle O\) az \(\displaystyle ABC\) háromszög körülírt körének középpontját, \(\displaystyle T\) az \(\displaystyle A\) pont \(\displaystyle BC\) egyenesre vett tükörképét, \(\displaystyle X\) az \(\displaystyle A\) pont inverzét a Feuerbach-körre nézve, \(\displaystyle D_A\) az \(\displaystyle AA'\) felezőpontját, \(\displaystyle K\) a \(\displaystyle BOC\) háromszög körülírt körének középpontját, \(\displaystyle P\) pedig az \(\displaystyle (ABC)\) kör \(\displaystyle B\)-beli és \(\displaystyle C\)-beli érintőinek metszéspontját.

Azonnal észrevehetjük, hogy \(\displaystyle P\) rajta van a \(\displaystyle (BOC)\) körön, sőt, \(\displaystyle OP\) átmérője a körnek, hiszen az érintők miatt a \(\displaystyle B,C\) pontok derékszögben látszanak az \(\displaystyle OP\) szakaszból. Illetve \(\displaystyle D_A\) is rajta van ezen a körön, hiszen \(\displaystyle P\) is rajta van a szimmediánon, és \(\displaystyle OD_A\perp AA'\) (mivel \(\displaystyle D_A\) a húr felezőpontja).

Most tekintsük az \(\displaystyle A\) középpontú \(\displaystyle r:=\sqrt{\dfrac{|AB|\cdot| AC|}{2}}\) sugarú inverziónak és az \(\displaystyle A\)-hoz tartozó szögfelezőre való tükrözés kompozícióját. Ezen transzformáció alatt minden \(\displaystyle K\) pont képét jelöljük \(\displaystyle K^*\)-al. Jegyezzük meg, hogy ez a transzformáció egy involúció, azaz \(\displaystyle (Q^*)^*=Q\). Rögtön megállapíthatjuk, hogy \(\displaystyle B^*=E\) és \(\displaystyle C^*=F\). Lássuk be, hogy \(\displaystyle D_A^*=D\). Az \(\displaystyle A'\) pont rajta van az \(\displaystyle (ABC)\) körön, amelynek képe az \(\displaystyle EF\) középvonal. Mivel az \(\displaystyle A\)-szimmedián egyenes képe az \(\displaystyle AD\) súlyvonal, az \(\displaystyle A'\) képe az \(\displaystyle EF\) középvonal és a súlyvonal metszéspontja, ami mellesleg az \(\displaystyle AD\) felezőpontja. Az inverzió miatt viszont \(\displaystyle A'\) képe az \(\displaystyle AD_A^*\) felezőpontja, hiszen

\(\displaystyle |AD_A^*|=\dfrac{r^2}{|AD_A|}=\dfrac{r^2}{\frac{|AA'|}{2}}=2\cdot|AA'^*|.\)

Ezzel beláttuk, hogy \(\displaystyle D_A^*=D\). Sőt, ebből az is látszik, hogy a \(\displaystyle (DEF)\) Feuerbach-kör képe éppen a \(\displaystyle (D_ABC)\) kör. Ezen a körön \(\displaystyle O\) is rajta van, így \(\displaystyle O^*\) rajta fekszik a Feuerbach-körön. Az \(\displaystyle (AEF)\) kör is átmegy \(\displaystyle O\)-n, így ennek a körnek a képe, azaz a \(\displaystyle BC\) egyenes is átmegy \(\displaystyle O^*\)-on. Tehát \(\displaystyle O^*\) csak is az \(\displaystyle A\)-hoz tartozó magasságvonal talppontja lehet. Mivel \(\displaystyle O^*\) az \(\displaystyle AT\) felezőpontja, ezért a korábbiakhoz hasonlóan \(\displaystyle T^*\) az \(\displaystyle AO\) szakasz felezőpontja lesz. Végül mi lesz \(\displaystyle X^*\)? \(\displaystyle A\) és \(\displaystyle X\) egymás inverzei a Feuerbach-körre nézve, így a transzformáció után a végtelen pont és \(\displaystyle X^*\) is egymás inverzei lesznek a \(\displaystyle (BD_AOCP)\) körre nézve (hiszen ez a kör a Feuerbach-kör képe). Azaz \(\displaystyle X^*\) ezen kör középpontja lesz, avagy az \(\displaystyle OP\) átmérő felezőpontja.

Térjünk rá a feladatra. Azt kell igazolni, hogy a \(\displaystyle T,D_A,X\) pontok kollineárisak. A transzformáció után ez ekvivalens azzal, hogy az \(\displaystyle A,T^*,D,X^*\) pontok egy körön vannak. Mivel \(\displaystyle AT^*\cap DX^*=O\), elég azt igazolni, hogy \(\displaystyle OD\cdot OX^*=OT^*\cdot OA\). Ám \(\displaystyle OA=2OT^*\) és \(\displaystyle OP=2OX^*\), így ez ekvivalens azzal, hogy \(\displaystyle OA^2=OD\cdot OP\), ami pont azt jelenti, hogy az \(\displaystyle OA\) érinti az \(\displaystyle (ADP)\) kört. Ezt könnyen be tudjuk látni. Az állítás ekvivalens azzal, hogy \(\displaystyle DAO\sphericalangle =DPA\sphericalangle\). Az izogonalitások miatt viszont \(\displaystyle DAO\sphericalangle=O^*AP\sphericalangle\), ahonnan a váltószögekből kapjuk, hogy \(\displaystyle O^*AP\sphericalangle=DPA\sphericalangle\). Készen vagyunk.

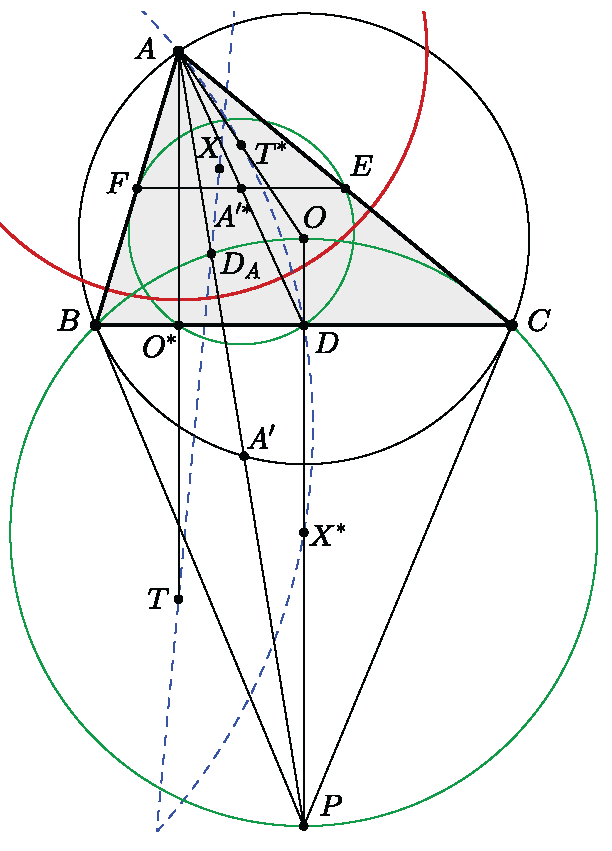
Megjegyzés: \(\displaystyle D_A\) az \(\displaystyle A\) csúcshoz tartozó Dumpty-pont.

Statisztika:

21 dolgozat érkezett.
7 pontot kapott:	Ali Richárd, Bodor Mátyás, Bui Thuy-Trang Nikolett, Diaconescu Tashi, Forrai Boldizsár, Gyenes Károly, Li Mingdao, Liu Zhe, Szakács Ábel, Vigh 279 Zalán, Vincze Marcell, Xiaoyi Mo.
6 pontot kapott:	Prohászka Bulcsú, Vödrös Dániel László.
5 pontot kapott:	1 versenyző.
4 pontot kapott:	1 versenyző.
3 pontot kapott:	1 versenyző.
0 pontot kapott:	3 versenyző.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2025. szeptemberi matematika feladatai