Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány
Már regisztráltál?
Új vendég vagy?

A B. 4009. feladat (2007. május)

B. 4009. Az ABC háromszög A és B csúcsából induló szögfelezője a szemközti oldalakat A1-ben, illetve B1-ben metszi. Az A1B1 félegyenesnek a háromszög körülírt körével alkotott metszéspontja P. Bizonyítsuk be, hogy

\frac{1}{PA} = \frac{1}{PB} + \frac{1}{PC}.

(5 pont)

A beküldési határidő 2007. június 15-én LEJÁRT.

Megoldás: Írjuk át a bizonyítandó állítást PB.PC=PA.PC+PA.PB alakba. A szokásos jelölések mellett jelölje R a körülírt kör sugarát, tXYZ az XYZ háromszög területét. Legyen továbbá t=tABC és q=PB1/A1B1, ekkor PA1/A1B1=1+q. A szögfelező-tételt felhasználva

\frac{t_{PBC}}{t}=\frac{t_{PBC}}{t_{B_1BC}}\cdot \frac{t_{B_1BC}}{t}=\frac{PA_1}{A_1B_1}\cdot \frac{B_1C}{AC}=(1+q)\frac{a}{a+c},

ezért

PB\cdot PC=\frac{2t_{PBC}}{\sin\alpha}=\frac{4Rt_{PBC}}{a}= \frac{4Rt(1+q)}{a+c}.

Hasonlóképpen kapjuk, hogy

PA\cdot PC=\frac{4Rt_{PAC}}{b}=\frac{4Rqt_{A_1AC}}{b}= \frac{4Rtq}{b}\cdot\frac{A_1C}{BC}=\frac{4Rtq}{b+c}.

A PAB háromszög területének meghatározásához jelölje az X pontnak az AB egyenestől vett távolságást mX, és legyen m=mC. Ekkor

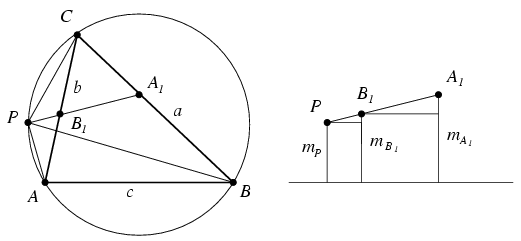
m_{A_1}=\frac{A_1B}{BC}\cdot m_C=\frac{cm}{b+c}\quad\hbox{\rm és}\quad m_{B_1}=\frac{B_1A}{AC}\cdot m_C=\frac{cm}{a+c}.

Ezért az ábráról leolvasható hasonlóságok alapján (az ábra az a>b esetet szemlélteti) mB1-mP=q(mA1-mB1), ahonnan

m_P=m_{B_1}-q(m_{A_1}-m_{B_1})=\frac{cm}{(a+c)(b+c)}\bigl(b+c-q(a-b)\bigr).

Következésképpen

PA\cdot PB=\frac{4Rt_{PAB}}{c}=\frac{4Rt}{c}\cdot\frac{m_P}{m}= \frac{4Rt}{(a+c)(b+c)}\bigl(b+c-q(a-b)\bigr),

tehát

PA\cdot PC+PA\cdot PB=\frac{4Rt}{(a+c)(b+c)}\bigl(q(a+c)+(b+c)-q(a-b)\bigr)=

=\frac{4Rt}{(a+c)(b+c)}(1+q)(b+c)=PB\cdot PC.

Statisztika:

8 dolgozat érkezett.
5 pontot kapott:Bogár 560 Péter, Dinh Van Anh, Fonyó Dávid, Honner Balázs, Tossenberger Anna, Wolosz János.
4 pontot kapott:Cseh Ágnes, Réti Dávid.

A KöMaL 2007. májusi matematika feladatai