 |
A B. 4069. feladat (2008. február) |
B. 4069. Az A és B pontokból, rendre a és b hosszú érintők húzhatók a k körhöz. A kör egy T pontjára teljesül, hogy az A, B, T pontok nem esnek egy egyenesre és
Bizonyítsuk be, hogy az A, B, T pontokra illeszkedő kör érinti k-t.
(5 pont)
A beküldési határidő 2008. március 17-én LEJÁRT.
Megoldás: Mivel az A, B, T pontok nem esnek egy egyenesre, AT/a=BT/b=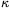
 1. A k kör középpontját jelöljük O-val, a sík egy X pontjából a k-hoz húzott érintőszakasz hosszát pedig jelölje x. A feladatban megfogalmazott állítás azonnal következik az alábbi általános észrevételből: tetszőleges 0<
1. A k kör középpontját jelöljük O-val, a sík egy X pontjából a k-hoz húzott érintőszakasz hosszát pedig jelölje x. A feladatban megfogalmazott állítás azonnal következik az alábbi általános észrevételből: tetszőleges 0<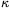
 1 esetén azon X pontok mértani helye a síkon, amelyekre XT/x=
1 esetén azon X pontok mértani helye a síkon, amelyekre XT/x=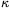 , egy olyan
, egy olyan kör T-től különböző pontjaival egyezik meg, amely áthalad a T ponton, középpontja pedig az OT egyenesre esik. Ezt fogjuk tehát bizonyítani.
Vegyük fel azt a derékszögű koordinátarendszert, amelynek középpontja O, és amelyben a T pont koordinátái T(1;0). Az X(u;v) pont pontosan akkor esik a k körön kívül, ha u2+v2>1, ekkor az OX egyenesnek a k-val alkotott metszéspontjai és
lesznek. Az X pontnak a k körre vonatkozó x2=XP.XQ hatványa tehát
Másrészt XT2=(u-1)2+v2, vagyis az XT/x=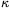 feltétel u2+v2
feltétel u2+v2 1 esetén ekvivalens az
1 esetén ekvivalens az
(u-1)2+v2=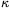 2(u2+v2-1)
2(u2+v2-1)
feltétellel, amit elemi átalakításokkal
alakra hozhatunk. 0<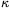 <1 esetén ez egy olyan T-n átmenő kör egyenlete, amelynek
<1 esetén ez egy olyan T-n átmenő kör egyenlete, amelynek középpontja az OT szakasz T-n túli meghosszabbítására esik,
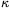 >1 esetén pedig egy olyan T-n átmenő kör egyenlete, amelynek
>1 esetén pedig egy olyan T-n átmenő kör egyenlete, amelynek középpontja az OT szakasz O-n túli meghosszabbítására esik. Mindkét esetben tehát egy olyan
körhöz jutottunk, amely k-t a T-ben érinti, és a T ponttól eltekintve azon kívül helyezkedik el. Ezzel állításunkat bebizonyítottuk.
Statisztika:
34 dolgozat érkezett. 5 pontot kapott: Bencs 111 Ferenc, Bodor Bertalan, Dinh Hoangthanh Attila, Dinh Van Anh, Éles András, Fonyó Dávid, Gévay Gábor, Grósz Dániel, Horváth 385 Vanda, Keresztfalvi Tibor, Kiss 243 Réka, Lovas Lia Izabella, Márkus Bence, Nagy 648 Donát, Perjési Gábor, Szabó 895 Dávid, Tossenberger Anna, Tubak Dániel, Varga 171 László. 4 pontot kapott: Bartha Zsolt, Csere Kálmán, Farkas Márton, Huszár Kristóf, Strenner Péter, Szalkai Balázs, Szórádi Márk, Tóth 369 László Márton, Véges Márton, Wang Daqian. 3 pontot kapott: 3 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 1 versenyző.
A KöMaL 2008. februári matematika feladatai
