A B. 4158. feladat (2009. február)

B. 4158. Egy kocka ABCD lapján az AB szakasz felezőpontja F. Vágjuk el a kockát egy, a CF szakaszon áthaladó síkkal úgy, hogy a B, illetve a D csúcsot tartalmazó részek térfogatának aránya 1:2 legyen. Mekkora szöget zár be ekkor a metsző sík az ABCD lappal?

(5 pont)

A beküldési határidő 2009. március 16-án LEJÁRT.

Megoldás: A kocka fedőlapja legyen XYZV az ábrán látható módon, az XY és ZV élek felezőpontja pedig E, illetve G. Ekkor az EZ szakasz párhuzamos az FC szakasszal, az F,C,E és Z pontokon áthaladó sík által levágott FBCEYZ hasáb térfogata pedig nyilván egynegyede a kocka térfogatának. Nyilván az XG szakasz is párhuzamos az FC szakasszal, az F,C,X és G pontokon áthaladó sík pedig szimmetria okok miatt felezi a kocka térfogatát. Az FEXCZG háromszög alapú ferde hasáb térfogata ezek szerint szintén egynegyede a kocka térfogatának. A metsző síkkal ennek a hasábnak a térfogatát is 1:2 arányban kell felosztanunk, vagyis annak az XE szakasz E-hez közelebbi H harmadolópontján (és a GZ szakasz Z-hez közelebbi J harmadolópontján) kell áthaladnia.

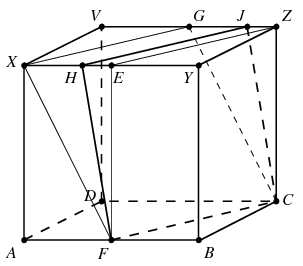
Vegyünk fel egy derékszögű (x;y;z) koordinátarendszert, melynek középpontja az A csúcs, a B,D,X csúcsok koordinátái pedig rendre B(1;0;0), D(0;1;0) és X(0;0;1). A z=0 egyenletű ABCD síkra merőleges u=(0;0;1) és az $x-\frac{1}{2}y+\frac{1}{6}z=\frac{1}{2}$ egyenletű FCJH síkra merőleges ${\bf v}=(1;-\frac{1}{2};\frac{1}{6})$ vektorok $\varphi$ szögét a skaláris szorzás segítségével a

$\cos\varphi=\frac{{\bf u}\cdot{\bf v}}{|{\bf u}|\cdot|{\bf v}|}= \frac{0\cdot 1-0\cdot\left(-\frac{1}{2}\right)+1\cdot \frac{1}{6}}{\sqrt{0^2+0^2+1^2}\cdot \sqrt{1^2+\left(-\frac{1}{2}\right)^2+\left(\frac{1}{6}\right)^2}}= \frac{1}{\sqrt{46}}$

képlet határozza meg. Innen $\varphi=\arccos\frac{1}{\sqrt{46}} \approx81,5^\circ$ , ennyi a két sík hajlásszöge is.

Statisztika:

59 dolgozat érkezett.

5 pontot kapott: Ágoston Péter, Ágoston Tamás, Bálint Dániel, Beke Lilla, Blázsik Zoltán, Bodor Bertalan, Böőr Katalin, Csizmadia Luca, Deák Zsolt, Éles András, Fonyó Dávid, Frankl Nóra, Horowitz Gábor, Huszár Kristóf, Keresztfalvi Tibor, Kiss 902 Melinda Flóra, Kovács 235 Gábor, Lenger Dániel, Lovas Lia Izabella, Maknics András, Márki Róbert, Márkus Bence, Mezei Márk, Nagy 648 Donát, Németh 217 Balázs, Perjési Gábor, Rácz Zoltán, Somogyi Ákos, Strenner Péter, Varga 171 László.

4 pontot kapott: Nagy 729 Krisztina, Prok Tamás, Scharle András, Szenczi Zoltán, Weisz Ágoston.

3 pontot kapott: 5 versenyző.

2 pontot kapott: 13 versenyző.

1 pontot kapott: 4 versenyző.

0 pontot kapott: 2 versenyző.

A KöMaL 2009. februári matematika feladatai

59 dolgozat érkezett.
5 pontot kapott:	Ágoston Péter, Ágoston Tamás, Bálint Dániel, Beke Lilla, Blázsik Zoltán, Bodor Bertalan, Böőr Katalin, Csizmadia Luca, Deák Zsolt, Éles András, Fonyó Dávid, Frankl Nóra, Horowitz Gábor, Huszár Kristóf, Keresztfalvi Tibor, Kiss 902 Melinda Flóra, Kovács 235 Gábor, Lenger Dániel, Lovas Lia Izabella, Maknics András, Márki Róbert, Márkus Bence, Mezei Márk, Nagy 648 Donát, Németh 217 Balázs, Perjési Gábor, Rácz Zoltán, Somogyi Ákos, Strenner Péter, Varga 171 László.
4 pontot kapott:	Nagy 729 Krisztina, Prok Tamás, Scharle András, Szenczi Zoltán, Weisz Ágoston.
3 pontot kapott:	5 versenyző.
2 pontot kapott:	13 versenyző.
1 pontot kapott:	4 versenyző.
0 pontot kapott:	2 versenyző.

Már regisztráltál?
Új vendég vagy?