A KöMaL 2009. februári matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2009. március 10-én LEJÁRT. |
K. 199. Dixi ötjegyű számokat rak sorba egy általa kitalált szabály szerint. Elsőként az utolsó számjegy szerint rakja csökkenő sorrendbe a számokat. Ha ez két szám esetén megegyezik, akkor az kerül előrébb, amelynek első számjegye kisebb. Ha ez is megegyezik, akkor a közbülső számjegyek szorzata szerinti csökkenő sorrendbe kerülnek a számok. (Dixi csak olyan számokat rak sorba, melyeknél ezek alapján egyértelműen eldönthető a sorrend.) Dixi egy papírra felírt hat számot a fent megfogalmazott szabályok szerint sorba rakva, azonban papírján elmosódott néhány számjegy (ezeket itt most betűkkel jelöltük), így ez olvasható rajta: 42348, A8318, 56B48, 8653C, 46585, D8655. A lehetőségeket végiggondolva tippelünk arra, hogy melyik volt a Dixi által sorbarakott hat szám (a tippünk minden számra egy-egy lehetséges értéket mond). Mennyi az esélye annak, hogy eltaláljuk Dixi összes számát?
(6 pont)
K. 200. Egy teniszversenyen 64 résztvevő van, és mindenki játszik a többiekkel mérkőzéseket (egy mérkőzés csak egy játszmából áll). Aki összegyűjt három vereséget, az kiesik. A győztes az, aki a végén bennmarad egyedül. Minimum, illetve maximum hány mérkőzésre kerülhet sor ezen a versenyen?
(6 pont)
K. 201. Hányféleképpen olvasható ki az ábrából a 2009, ha mindig csak élben szomszédos mezőkre léphetünk?
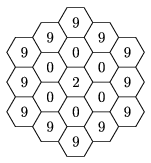
(6 pont)
K. 202. Szorozzuk meg önmagával a 99 999 989 999 számot. Állapítsuk meg számológép nélkül, hogy az eredményben hány darab 9-es számjegy van.
(6 pont)
K. 203. Egy függvényről azt tudjuk, hogy minden x 0 esetén
0 esetén
Határozzuk meg f(2) értékét.
(6 pont)
K. 204. Az alábbi ábrát akarjuk elkészíteni. Mennyi lesz a satírozott terület és a nem satírozott terület aránya? (Az ábrát határoló görbék félkörök, az átmérőn látható pontok harmadolópontok.)
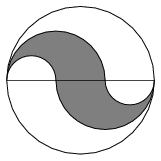
(6 pont)
 |
C-jelű feladatokA beküldési határidő 2009. március 16-án LEJÁRT. |
C. 975. Az ABC háromszögben a C csúcsból húzott magasság az AB oldalt T-ben metszi. Az AC és a BC oldalakra kifelé olyan derékszögű CAD és CBE háromszögeket rajzolunk, amelyekben A-nál, illetve B-nél van a derékszög. Tudjuk továbbá, hogy AD=TB és BE=TA. Igazoljuk, hogy .
(5 pont)
C. 976. Adjuk meg azt a legszűkebb intervallumot, ahová három pozitív szám összegének és a reciprokaik összegének szorzata eshet.
(5 pont)
C. 977. Egy vállalkozó 12 millió Ft kedvezményes hitelt vett fel évi 8%-os fix kamattal. Mennyi lesz a tartozása 10 év múlva, ha évente 1,2 millió forintot tud törleszteni?
(5 pont)
C. 978. Egy kávézóban három kétszemélyes asztalnál összesen hatan foglalnak helyet. Közülük hárman kávét, hárman teát isznak. Mekkora a valószínűsége annak, hogy van olyan asztal, ahol mind a ketten teát isznak?
(5 pont)
C. 979. Piros alapon fehér pöttyös labdánkon harminc (gömbsüveg alakú) pötty található. A labda főkörének kerülete 54 cm, a pöttyök kerülete 11 cm. A labda felszínének hány százaléka pötty?
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2009. március 16-án LEJÁRT. |
B. 4152. Adott az számoknak n darab különböző részhalmaza. Bizonyítsuk be, hogy van olyan szám, amelyet minden halmazból elhagyva, a megmaradó halmazok továbbra is különbözőek.
(4 pont)
B. 4153. Az ABC háromszög körülírt körének középpontja O, magasságpontja M. Vegyük föl az E és F pontokat az AC és AB félegyeneseken A-tól AO, illetve AM távolságra. Bizonyítsuk be, hogy ekkor EF=AO.
(4 pont)
B. 4154. Egy klasszikus feladat: Egy kör alakú városfalon 12 őr teljesít szolgálatot. Délben mindegyikük elindul az őrhelyéről a falon valamelyik irányba olyan sebességgel, amellyel egy óra alatt kerülné meg a várost. Ha két őr szembetalálkozik, akkor sarkon fordulnak és változatlan sebességgel haladnak tovább az ellenkező irányba. Bizonyítsuk be, hogy pontban éjfélkor minden egyes őr a saját őrhelyén lesz.
(5 pont)
B. 4155. Oldjuk meg a következő egyenletet:
a2b2+b2c2+c2a2+a2+b2+c2+4(a+b+c)+12=6abc+4(ab+bc+ca).
(5 pont)
B. 4156. Oldjuk meg az alábbi egyenletet:
(3 pont)
B. 4157. Oldjuk meg az alábbi egyenletet: [x]=x4-2x2.
Erdélyi versenyfeladat nyomán
(4 pont)
B. 4158. Egy kocka ABCD lapján az AB szakasz felezőpontja F. Vágjuk el a kockát egy, a CF szakaszon áthaladó síkkal úgy, hogy a B, illetve a D csúcsot tartalmazó részek térfogatának aránya 1:2 legyen. Mekkora szöget zár be ekkor a metsző sík az ABCD lappal?
(5 pont)
B. 4159. Az ABC háromszögben a=2b. Szerkesszük meg a háromszöget, ha adott az A és B csúcsa és egy egyenes, amelyre a C csúcs illeszkedik.
(3 pont)
B. 4160. Van-e olyan korlátos ponthalmaz a síkon, amelynek végtelen sok szimmetriatengelye van, de nem középpontosan szimmetrikus?
Javasolta: Pósa Lajos
(5 pont)
B. 4161. Tegyük föl, hogy a természetes számok halmazának véges sok pozitív elemét elhagyva egy olyan S halmazt kaptunk, amely zárt az összeadásra. Legyen az S egyik eleme k. Hány olyan eleme van S-nek, amiből k-t kivonva S-hez nem tartozó számot kapunk?
(3 pont)
 |
A-jelű feladatokA beküldési határidő 2009. március 16-án LEJÁRT. |
A. 473. Mutassuk meg, hogy az egyenlő területű gömbháromszögek átdarabolhatók egymásba, azaz bármelyik két, egyenlő területű gömbháromszöget feloszthatjuk véges sok gömbi sokszögre olymódon, hogy a két felbontás ugyanannyi darabból álljon, és ezekben a megfelelő darabok egybevágók legyenek egymással.
(5 pont)
A. 474. A Q pont a konvex sokszög belsejében helyezkedik el. Igazoljuk, hogy
(Az indexeket modulo n értjük, azaz P0=Pn és Pn+1=P1.)
(5 pont)
A. 475. Egy szabályos n-szög csúcsaihoz valós számokat rendeltünk úgy, hogy az n szám összege pozitív. Ha három egymás után következő szám x, y, illetve z, továbbá y<0, akkor ezeket kicserélhetjük rendre az x+y, -y, z+y számokra. Ezt a műveletet mindaddig ismételgetjük, amíg csak van a számok között legalább egy negatív.
Döntsük el, hogy vajon minden esetben befejeződik-e ez az eljárás véges sok lépésben.
(5 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)
