A B. 4388. feladat (2011. október)

B. 4388. Az ABC hegyesszögű háromszög AB oldalának belső pontja D. A D ponton keresztül az AC oldallal húzott párhuzamos a BC oldalt az E, a D-n keresztül a BC oldallal húzott párhuzamos pedig az AC oldalt az F pontban metszi. Az ADF és BDE körök második metszéspontja G. Igazoljuk, hogy ABEF akkor és csak akkor húrnégyszög, ha G rajta van a CD szakaszon.

Javasolta: Miklós Szilárd (Herceghalom)

(4 pont)

A beküldési határidő 2011. november 10-én LEJÁRT.

Megoldás. Az $\displaystyle ADF$ és $\displaystyle DBE$ háromszögek hasonlóak az $\displaystyle ABC$ háromszöghöz; a szokásos jelölésekkel $\displaystyle AFD\sphericalangle=DEB\sphericalangle=\gamma$. Az $\displaystyle ADF$, illetve $\displaystyle DEB$ körökhöz a $\displaystyle D$ pontban húzott érintők tehát az $\displaystyle AB$ egyenessel $\displaystyle \gamma$ szöget zárnak be. Mivel $\displaystyle \gamma<90^\circ$, ezek a körök az $\displaystyle AB$ egyenesnek $\displaystyle C$-t tartalmazó oldalán metszik egymást, így a $\displaystyle G$ pont is az $\displaystyle AB$ egyenesnek erre az oldalára esik.

Az $\displaystyle ABEF$ négyszög pontosan akkor húrnégyszög, ha $\displaystyle CEF\sphericalangle=\alpha$ és $\displaystyle CFE\sphericalangle=\beta$ (ez a két utóbbi feltétel persze ekvivalens egymással), vagyis ha az $\displaystyle EF$ egyenes az $\displaystyle ADF$ és $\displaystyle DBE$ körök közös érintője; ekkor a $\displaystyle G$ pont nyilván az $\displaystyle EFD$ háromszög belsejébe esik. Feltehetjük tehát, hogy a $\displaystyle G$ pont az $\displaystyle ABC$ háromszög belső pontja, ellenkező esetben ugyanis sem $\displaystyle ABEF$ nem lehet húrnégyszög, sem pedig $\displaystyle G$ nem lehet rajta a $\displaystyle CD$ szakaszon. Ekkor utalhatunk az alábbi ábrára. Mivel $\displaystyle EGD\sphericalangle=180^\circ-\beta$ és $\displaystyle FGD\sphericalangle=180^\circ-\alpha$, látható, hogy $\displaystyle EGF\sphericalangle=180^\circ-\gamma$, vagyis az $\displaystyle ECFG$ négyszög húrnégyszög.

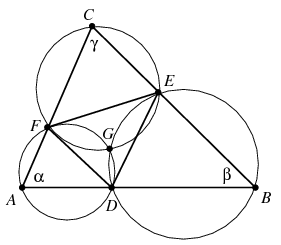
Ekkor tehát így érvelhetünk. Az $\displaystyle ABEF$ négyszög pontosan akkor húrnégyszög, ha $\displaystyle CFE\sphericalangle=\beta$, vagyis ha $\displaystyle CGE\sphericalangle=\beta$. Figyelembe véve, hogy $\displaystyle EGD\sphericalangle=180^\circ-\beta$, ez ekvivalens azzal, hogy a $\displaystyle CGD$ szög egyenesszög, vagyis hogy a $\displaystyle G$ pont rajta van a $\displaystyle CD$ szakaszon.

Statisztika:

63 dolgozat érkezett.
4 pontot kapott:	Barna István, Bingler Arnold, Bősze Zsuzsanna, Demeter Dániel, Demeter Márton, Dinev Georgi, Dolgos Tamás, Fehér Zsombor, Fonyó Viktória, Forrás Bence, Garamvölgyi Péter, Gasparics Fanni, Gyarmati Máté, Havasi 0 Márton, Janzer Olivér, Kiss 065 Eszter, Kiss 902 Melinda Flóra, Kúsz Ágnes, Leitereg András, Leitereg Miklós, Maga Balázs, Makk László, Máthé László, Medek Ákos, Mester Márton, Mihálykó András, Nagy Anna Noémi, Nagy Róbert, Németh 722 Noémi, Nguyen Anh Tuan, Ódor Gergely, Papp Roland, Sagmeister Ádám, Somogyvári Kristóf, Szabó 789 Barnabás, Szilágyi Gergely Bence, Tekeli Tamás, Tran Duy An, Tulassay Zsolt, Varga 149 Imre Károly, Varnyú József, Viharos Andor, Weisz Ambrus, Wiandt Zsófia, Zilahi Tamás, Zsiros Ádám.
3 pontot kapott:	8 versenyző.
2 pontot kapott:	4 versenyző.
0 pontot kapott:	5 versenyző.

A KöMaL 2011. októberi matematika feladatai