A B. 4584. feladat (2013. december)

B. 4584. Egy parallelogramma két átellenes csúcsán át fektessünk egy-egy olyan egyenest, amelyek a parallelogramma oldalainak meghosszabbításait két-két pontban metszik. Bizonyítsuk be, hogy ez a négy metszéspont egy trapéz négy csúcsa.

Javasolta: Moussong Gábor (Budapest)

(4 pont)

A beküldési határidő 2014. január 10-én LEJÁRT.

1. megoldás. Betűzzük a paralelogrammát és a metszéspontokat az ábra szerint. Azt akarjuk megmutatni, hogy az PR és az SQ szakasz párhuzamos egymással. Mivel AB||CD és AD||BC, a következők ekvivalensek:

(a) az PR és az SQ szakasz párhuzamos egymással;

(b) a BRB és DQS háromszögek hasonlók;

(c) .

A (c) állítást fogjuk igazolni.

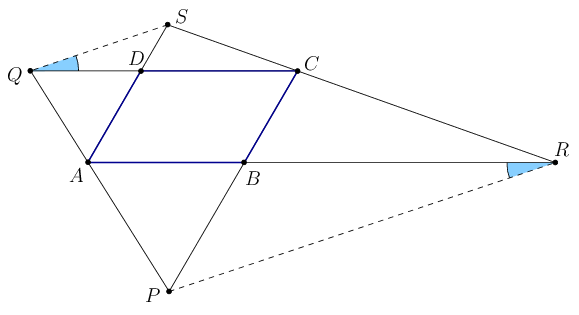
A PBA és ADQ háromszögek hasonlók, mert megfelelő oldalaik párhuzamosak, ezért

(1)

A CBR és SDC háromszögek is hasonlók, és

(2)

A paralelogramma szemközti oldalai egyenlők, így

(3).

Az (1), (2) és (3) szorzata a (c) állítás.

2. megoldás. Alkalmazzuk a Papposz-tételt az A,P,Q és C,S,R ponthármasokra.

Statisztika:

133 dolgozat érkezett.
4 pontot kapott:	90 versenyző.
3 pontot kapott:	33 versenyző.
2 pontot kapott:	4 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	4 versenyző.

A KöMaL 2013. decemberi matematika feladatai