 |
A B. 4693. feladat (2015. február) |
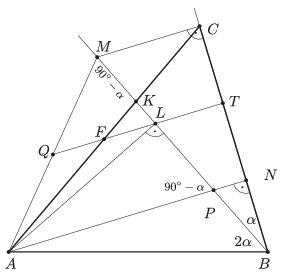
B. 4693. Az \(\displaystyle ABC\) háromszög \(\displaystyle AC\) oldalán lévő \(\displaystyle K\) pontra \(\displaystyle AK=2KC\) és \(\displaystyle ABK\sphericalangle = 2KBC\sphericalangle\) teljesül. Jelölje \(\displaystyle F\) az \(\displaystyle AC\) oldal felezőpontját, az \(\displaystyle A\) pont \(\displaystyle BK\) szakaszra eső merőleges vetületét pedig \(\displaystyle L\). Igazoljuk, hogy az \(\displaystyle FL\) és \(\displaystyle BC\) egyenesek merőlegesek egymásra.
(5 pont)
A beküldési határidő 2015. március 10-én LEJÁRT.
Megoldási ötlet: Tükrözzük az \(\displaystyle A\)-t a \(\displaystyle BK\) egyenesére.
Megoldás. Legyen \(\displaystyle KBC\sphericalangle =\alpha\). Ekkor a feltételek szerint \(\displaystyle ABK\sphericalangle =2\alpha\). E szögek segítségével felírva az \(\displaystyle ABK\) és \(\displaystyle KBC\) háromszögek területét, kapjuk hogy
\(\displaystyle T_{ABK} =\frac{AB\cdot BK\cdot \sin 2\alpha}{2},\)
valamint
\(\displaystyle T_{KBC} =\frac{BK\cdot BC\cdot \sin \alpha}{2}.\)
A két háromszög \(\displaystyle B\) csúcshoz tartozó magassága közös, \(\displaystyle B\)-vel szemközti oldalaik aránya pedig \(\displaystyle 2:1\), mert \(\displaystyle K\) az \(\displaystyle AC\) oldal harmadolópontja. Ezért \(\displaystyle T_{ABK}:T_{KBC}=2:1\). Ebből a \(\displaystyle \sin 2\alpha =2\sin \alpha \cos \alpha\) azonosságot is felhasználva kapjuk, hogy
\(\displaystyle AB\cdot BK\cdot \sin \alpha \cos \alpha =BK\cdot BC\cdot \sin \alpha, \)
vagyis (\(\displaystyle \sin\alpha\ne 0\) miatt) \(\displaystyle \cos \alpha =\frac{BC}{AB}\).
Legyen \(\displaystyle M\) a \(\displaystyle B\)-ből induló \(\displaystyle BK\) félegyenesnek az a pontja, melyre \(\displaystyle BM=BA\). Ekkor \(\displaystyle \cos \alpha =\frac{BC}{BM}\), ezért \(\displaystyle BCM\sphericalangle =90^{\circ}\). Továbbá az \(\displaystyle ABM\) háromszög egyenlőszárú, szárszöge \(\displaystyle 2\alpha\), ezért alapon fekvő szögei \(\displaystyle MAB\sphericalangle =AMB\sphericalangle = 90^{\circ}-\alpha\).
Legyen az \(\displaystyle A\)-ból \(\displaystyle BC\)-re állított merőleges talppontja \(\displaystyle N\), az \(\displaystyle AN\) és \(\displaystyle BK\) szakaszok metszéspontja pedig \(\displaystyle P\). A \(\displaystyle PNB\) derékszögű háromszög egyik hegyesszöge \(\displaystyle \alpha\), ezért a másik hegyesszög \(\displaystyle BPN\sphericalangle = 90^{\circ}-\alpha\). Ekkor \(\displaystyle MPA\sphericalangle =90^{\circ}-\alpha\) is, mert \(\displaystyle MPA\sphericalangle\) és \(\displaystyle BPN\sphericalangle\) csúcsszögek, tehát egyenlőek. Ez azt jelenti, hogy az \(\displaystyle APM\) háromszög is egyenlőszárú, mert \(\displaystyle M\)-nél és \(\displaystyle P\)-nél lévő szögei megegyeznek. Ezért az alaphoz tartozó magassága, \(\displaystyle AL\), felezi az \(\displaystyle MP\) alapot, tehát \(\displaystyle L\) az \(\displaystyle MP\) szakasz felezőpontja.
Legyen az \(\displaystyle AM\) szakasz felezőpontja \(\displaystyle Q\). Ekkor \(\displaystyle QL\) az \(\displaystyle APM\), \(\displaystyle QF\) pedig az \(\displaystyle AMC\) háromszög középvonala. A középvonalak párhuzamosak a háromszögek megfelelő oldalaival, azaz \(\displaystyle AP\)-vel, illetve \(\displaystyle MC\)-vel. E két utóbbi viszont egymással is párhuzamos, mert mindkettő merőleges \(\displaystyle BC\)-re. Tehát \(\displaystyle QF\) és \(\displaystyle QL\) is merőlegesek \(\displaystyle BC\)-re. Vagyis a \(\displaystyle Q\)-ból \(\displaystyle BC\)-re állított merőleges tartalmazza \(\displaystyle F\)-et és \(\displaystyle L\)-et is, ezért \(\displaystyle FL\) is merőleges \(\displaystyle BC\)-re, ami épp a bizonyítandó állítás.
Czirkos Angéla (Kecskemét, Bolyai J. Gimn., 10. évf.) dolgozata alapján
Statisztika:
34 dolgozat érkezett. 5 pontot kapott: Andi Gabriel Brojbeanu, Baran Zsuzsanna, Cseh Kristóf, Csépai András, Czirkos Angéla, Eper Miklós, Fekete Panna, Gáspár Attila, Geng Máté, Gyulai-Nagy Szuzina, Kerekes Anna, Keresztfalvi Bálint, Kocsis Júlia, Kovács 101 Dávid Péter, Leitereg Miklós, Mócsy Miklós, Nagy Kartal, Nagy-György Pál, Németh 123 Balázs, Polgár Márton, Porupsánszki István, Sal Kristóf, Schrettner Bálint, Schwarcz Tamás, Szebellédi Márton, Vághy Mihály, Varga-Umbrich Eszter, Várkonyi Dorka, Vu Mai Phuong, Wiandt Péter, Williams Kada. 2 pontot kapott: 3 versenyző.
A KöMaL 2015. februári matematika feladatai
