A B. 4708. feladat (2015. április)

B. 4708. Az \(\displaystyle ABC\) hegyesszögű háromszög körülírt körének középpontja \(\displaystyle O\), magasságpontja \(\displaystyle M\). Tükrözzük az \(\displaystyle A\) pontot a \(\displaystyle BC\) oldal felezőmerőlegesére, a \(\displaystyle B\) pontot a \(\displaystyle CA\) oldal felezőmerőlegesére, végül a \(\displaystyle C\) pontot az \(\displaystyle AB\) oldal felezőmerőlegesére, a tükörképek rendre \(\displaystyle A_1\), \(\displaystyle B_1\), \(\displaystyle C_1\). Legyen az \(\displaystyle A_1B_1C_1\) háromszög beírt körének középpontja \(\displaystyle K\). Bizonyítsuk be, hogy az \(\displaystyle O\) pont felezi az \(\displaystyle MK\) szakaszt.

Javasolta: Bíró Bálint (Eger)

(5 pont)

A beküldési határidő 2015. május 11-én LEJÁRT.

Megoldási ötlet: 1. Rajzoljuk meg a talpponti háromszöget. 2. Számoljuk ki a körülírt kör íveihez tartozó kerületi szögeket.

Megoldás. Legyen az \(\displaystyle ABC\) háromszög magasságvonalainak a \(\displaystyle k\) körülírt körrel való, a csúcsoktól különböző metszéspontja rendre \(\displaystyle A_2\), \(\displaystyle B_2\) és \(\displaystyle C_2\). Mivel \(\displaystyle AA_2\) a \(\displaystyle k\) kör \(\displaystyle BC\)-re merőleges húrja, ezért ennek \(\displaystyle f_a\) felezőmerőlegese átmegy \(\displaystyle O\)-n és merőleges \(\displaystyle BC\) felezőmerőlegesére is. Vizsgáljuk meg, mi lesz \(\displaystyle A_2\)-nek az \(\displaystyle O\)-ra vonatkozó tükörképe. Ismert, hogy egy pontra vonatkozó középpontos tükrözés helyettesíthető két olyan egyenesre vonatkozó tengelyes tükrözés egymásutánjával, melyek egymást merőlegesen metszik az adott pontban. Ezért ha \(\displaystyle A_2\)-t tükrözzük \(\displaystyle f_a\)-ra, majd a képét, \(\displaystyle A\)-t, \(\displaystyle BC\) felezőmerőlegesére, akkor a kapott \(\displaystyle A_1\) pont megegyezik \(\displaystyle A_2\)-nek az \(\displaystyle O\)-ra vonatkozó tükörképével (1. ábra). Ugyanígy látható be, hogy a \(\displaystyle B_2\), illetve \(\displaystyle C_2\) pontok \(\displaystyle O\)-ra vonatkozó tükörképe \(\displaystyle B_1\), illetve \(\displaystyle C_1\).

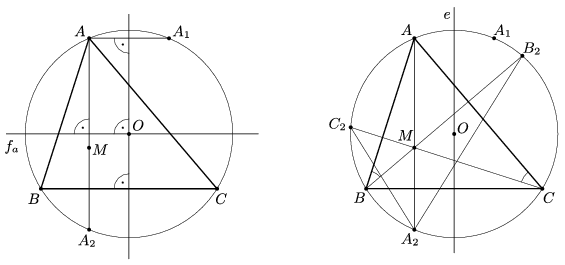
1. ábra                                                                       2. ábra

Tehát az \(\displaystyle A_1B_1C_1\) háromszög \(\displaystyle O\)-ra vonatkozó tükörképe az \(\displaystyle A_2B_2C_2\) háromszög. Ezért \(\displaystyle K\)-nak az \(\displaystyle O\)-ra vonatkozó tükörképe megegyezik az \(\displaystyle A_2B_2C_2\) háromszög beírt körének \(\displaystyle L\) középpontjával. Mivel \(\displaystyle O\) nyilván felezi az \(\displaystyle LK\) szakaszt, ezért feladatunk állításának igazolásához elegendő megmutatnunk, hogy \(\displaystyle M\equiv L\), ami ekvivalens azzal, hogy az \(\displaystyle A_2B_2C_2\) háromszögben az \(\displaystyle ABC\) háromszög magasságvonalai belső szögfelezők.

Legyen az \(\displaystyle ABC\) háromszög \(\displaystyle A\)-nál lévő szöge \(\displaystyle \alpha\). Mivel \(\displaystyle BB_2\perp AC\) és \(\displaystyle CC_2\perp AB\), ezért \(\displaystyle ABB_2\sphericalangle =90^{\circ}-\alpha =ACC_2\sphericalangle\). A \(\displaystyle k\) körben a kerületi szögek tétele miatt \(\displaystyle AA_2B_2\sphericalangle =ABB_2\sphericalangle \) és \(\displaystyle AA_2C_2\sphericalangle =ACC_2\sphericalangle\), tehát \(\displaystyle AA_2B_2\sphericalangle =AA_2C_2\sphericalangle \) (2. ábra). Vagyis \(\displaystyle AA_2\) felezi a \(\displaystyle C_2A_2B_2\) szöget. Ugyanígy látható be, hogy \(\displaystyle BB_2\) és \(\displaystyle CC_2\) is szögfelezők, s ezzel feladatunk állítását igazoltuk.

Nagy Dávid Paszkál (Budapesti Fazekas M. Gyak. Ált. Isk. és Gimn., 9. évf.) dolgozatát felhasználva

Statisztika:

38 dolgozat érkezett.
5 pontot kapott:	Baran Zsuzsanna, Bodolai Előd, Cseh Kristóf, Csépai András, Döbröntei Dávid Bence, Fekete Panna, Imolay András, Katona Dániel, Kerekes Anna, Keresztfalvi Bálint, Kocsis Júlia, Kovács 162 Viktória, Kovács Kitti Fanni, Lajkó Kálmán, Lakatos Ádám, Leitereg Miklós, Molnár-Sáska Zoltán, Nagy Ábel, Nagy-György Pál, Németh 123 Balázs, Olexó Gergely, Polgár Márton, Schrettner Bálint, Schwarcz Tamás, Szebellédi Márton, Török Zsombor Áron, Vághy Mihály, Vankó Miléna, Williams Kada.
4 pontot kapott:	Czirkos Angéla, Gáspár Attila, Glasznova Maja, Sal Kristóf.
3 pontot kapott:	1 versenyző.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2015. áprilisi matematika feladatai