 |
A B. 4906. feladat (2017. november) |
B. 4906. Az \(\displaystyle ABCD\) konvex négyszög \(\displaystyle BC\) és \(\displaystyle CD\) oldalainak felezőpontja rendre \(\displaystyle E\) és \(\displaystyle F\). Az \(\displaystyle AE\), \(\displaystyle EF\) és \(\displaystyle AF\) szakaszok a négyszöget négy olyan háromszögre bontják, melyek területeinek mérőszáma négy egymást követő egész szám. Legfeljebb mekkora lehet az \(\displaystyle ABD\) háromszög területe?
Javasolta: Róka Sándor (Nyíregyháza)
(5 pont)
A beküldési határidő 2017. december 11-én LEJÁRT.
Megoldás. A háromszögek területe \(\displaystyle n\), \(\displaystyle n+1\), \(\displaystyle n+2\), \(\displaystyle n+3\) valamely \(\displaystyle n\) pozitív egész számra, ezért az \(\displaystyle ABCD\) konvex négyszög területe \(\displaystyle 4n+6\). Mivel \(\displaystyle EF\) a \(\displaystyle BCD\) háromszög középvonala, ezért a \(\displaystyle BCD\) háromszög területe 4-szerese az \(\displaystyle ECF\) háromszögének, azaz legalább \(\displaystyle 4n\). Az \(\displaystyle ABD\) háromszög területe \(\displaystyle t_{ABCD}-t_{BCD}\leq (4n+6)-4n=6\).
Azt kaptuk, hogy az \(\displaystyle ABD\) háromszög területe legfeljebb 6. Ez elérhető például úgy, ha az \(\displaystyle ABCD\) négyszög olyan trapéz, melyre \(\displaystyle AB=6\), \(\displaystyle DC=4\) és a trapéz magassága 2.
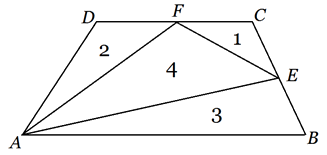
Ekkor \(\displaystyle t_{ABE}=\frac{6\cdot1}{2}=3\), \(\displaystyle t_{CFE}=\frac{2\cdot1}{2}=1\), \(\displaystyle t_{FDA}=\frac{2\cdot2}{2}=2\), \(\displaystyle t_{AEF}=t_{ABCD}-3-1-2=\frac{(6+4)\cdot2}{2}-6=10-6=4\). Vagyis a trapézt valóban négy olyan háromszögre bontottuk, melyek területeinek mérőszáma négy egymást követő egész szám, és az \(\displaystyle ABD\) háromszög területe eléri a lehetséges felső határt, amikor a terület 6.
Statisztika:
100 dolgozat érkezett. 5 pontot kapott: Beke Csongor, Busa 423 Máté, Csépányi István, Csertán András, Csiszár Zoltán, Csizmadia Viktória, Csóka Zoárd, Daróczi Sándor, Dobák Dániel, Döbröntei Dávid Bence, Fülöp Anna Tácia, Füredi Erik Benjámin, Gáspár Attila, Geretovszky Anna, Győrffi Ádám György, Győrffy Ágoston, Győrffy Johanna, Harsányi Benedek, Jánosik Máté, Janzer Orsolya Lili, Lukács Lilla Réka, Molnár Bálint, Molnár-Sáska Zoltán, Nagy Nándor, Noszály Áron, Olosz Adél, Pituk Gábor, Saár Patrik, Scheidler Barnabás, Schrettner Jakab, Soós 314 Máté, Szabó 417 Dávid, Szabó 864 Blanka, Szemerédi Levente, Tiderenczl Dániel, Tiszay Ádám, Tóth Ábel, Tóth-Rohonyi Iván, Tubak Dániel, Velkey Vince, Weisz Máté, Zólomy Kristóf, Zsigri Bálint. 4 pontot kapott: 48 versenyző. 3 pontot kapott: 6 versenyző. 2 pontot kapott: 3 versenyző.
A KöMaL 2017. novemberi matematika feladatai
