A B. 5067. feladat (2019. december)

B. 5067. Az \(\displaystyle ABC\) hegyesszögű háromszög \(\displaystyle AB\) oldalának felezőpontja \(\displaystyle F\), az \(\displaystyle F\)-re illeszkedő \(\displaystyle e\) egyenes felezi \(\displaystyle ABC\) kerületét. Az \(\displaystyle e\) egyenes a \(\displaystyle BC\) és \(\displaystyle CA\) oldalegyeneseket rendre \(\displaystyle D\) és \(\displaystyle E\) pontokban metszi. Mutassuk meg, hogy az \(\displaystyle AB\)-re \(\displaystyle F\)-ben állított merőleges, a \(\displaystyle BC\)-re \(\displaystyle D\)-ben állított merőleges, és a \(\displaystyle CA\)-ra \(\displaystyle E\)-ben állított merőleges egyenesek egy pontban metszik egymást.

(5 pont)

A beküldési határidő 2020. január 10-én LEJÁRT.

1. megoldás. Az \(\displaystyle A\) és \(\displaystyle B\) pontok szerepe szimmetrikus, ezért feltehetjük, hogy \(\displaystyle AC\le BC\). Ha \(\displaystyle AC=BC\), akkor az \(\displaystyle e\) átmegy \(\displaystyle C\)-n és merőleges \(\displaystyle AB\)-re, a \(\displaystyle C,D,E\) pontok egybeesnek, így az állítás teljesül. A továbbiakban azt az esetet vizsgáljuk, ha \(\displaystyle AC<BC\).

Legyen \(\displaystyle f\) a \(\displaystyle BCA\sphericalangle\) külső szögfelezője, és a \(\displaystyle BC\) szakasz \(\displaystyle C\)-n túli meghosszabbításán legyen \(\displaystyle A'\) az a pont, amelyre \(\displaystyle AC=A'C\). Az \(\displaystyle A'AC\) háromszög egyenlő szárú, ezért az \(\displaystyle A\) és az \(\displaystyle A'\) pont szimmetrikus \(\displaystyle f\)-re. A feltétel szerint az \(\displaystyle e\) egyenes felezi a háromszög kerületét, vagyis \(\displaystyle FB+BD=DC+CA+AF\). Mivel \(\displaystyle AF=FB\) és \(\displaystyle CA=CA'\), az is igaz, hogy \(\displaystyle BD=DC+CA=DC+CA'=DA'\), tehát a \(\displaystyle D\) pont felezi az \(\displaystyle BA'\) szakaszt. Az \(\displaystyle ABA'\) háromszögben az \(\displaystyle FD\) szakasz az \(\displaystyle A'A\) oldallal párhuzamos középvonal, tehát \(\displaystyle FD\parallel AA'\). Mivel \(\displaystyle AC=A'C\), a párhuzamos szelők tétele miatt \(\displaystyle CD=CE\), és emiatt \(\displaystyle D\) és \(\displaystyle E\) szimmetrikus \(\displaystyle f\)-re.

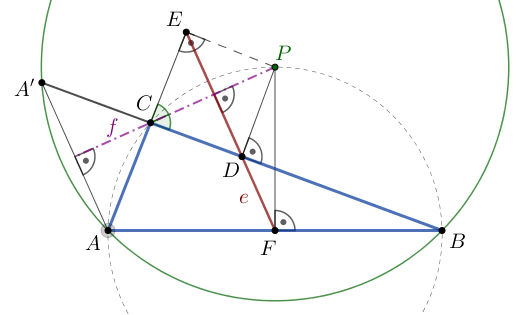
Legyen \(\displaystyle P\) az \(\displaystyle ABA'\) háromszög köré írt kör középpontja; ezen átmennek az \(\displaystyle AB\), \(\displaystyle BA'\) és \(\displaystyle AA'\) szakaszok felezőmerőlegesei, másképpen az \(\displaystyle AB\)-re \(\displaystyle F\)-ben állított merőleges, a \(\displaystyle BC\)-re \(\displaystyle D\)-ben állított merőleges és \(\displaystyle f\). A \(\displaystyle CDP\) háromszög \(\displaystyle f\)-re vonatkozó tükörképe a \(\displaystyle CEP\) háromszög, ezért \(\displaystyle CEP\sphericalangle=CDP\sphericalangle=90^\circ\), tehát a \(\displaystyle CA\)-ra \(\displaystyle E\)-ben állított merőleges egyenes is átmegy \(\displaystyle P\)-n.

Megjegyzés. Jól ismert, hogy az \(\displaystyle f\) szögfelező és az \(\displaystyle AB\) oldal felezőmerőlegese az \(\displaystyle ABC\) háromszög köré írt kör \(\displaystyle BCA\) ívének felezőpontjában metszi egymást.

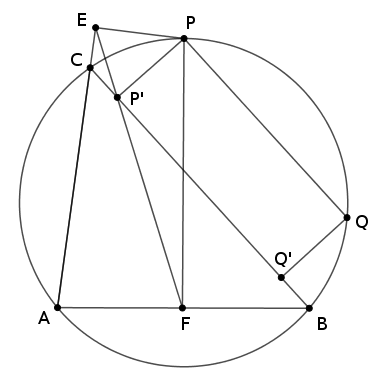
2. megoldás az \(\displaystyle AC < BC\) esetre. A háromszög körülírt körén a \(\displaystyle C\) pontot tartalmazó \(\displaystyle AB\) körív \(\displaystyle P\) felezőpontjáról megmutatjuk, hogy mindhárom egyenesen rajta van. Az \(\displaystyle AB\) felezőmerőlegese esetében ez nyilvánvaló. A \(\displaystyle P\) ponton átmenő, a \(\displaystyle BC\) oldallal párhuzamos egyenes messe a kört a \(\displaystyle P\)-től különböző \(\displaystyle Q\) pontban. A \(\displaystyle P\) és \(\displaystyle Q\) merőleges vetülete a \(\displaystyle BC\) oldalon \(\displaystyle P'\), illetve \(\displaystyle Q'\). Ekkor \(\displaystyle P'Q'=PQ\), \(\displaystyle CP'=Q'B\). A kerületi szögek tétele szerint (a szokásos jelölésekkel):

\(\displaystyle QBP\sphericalangle = QAP \sphericalangle = \alpha - 2PAC\sphericalangle = \alpha - 2PBC\sphericalangle = \alpha - 2(PBA\sphericalangle -\beta) = \alpha - 2((180^{\circ} - \gamma)/2 -\beta) = \alpha + \gamma +2\beta - 180^{\circ} = \beta. \)

Így \(\displaystyle P'Q'=PQ=AC\), ezért \(\displaystyle AC+CP'=P'Q'+Q'B\), tehát \(\displaystyle P'\equiv D\), azaz \(\displaystyle P\) illeszkedik a \(\displaystyle BC\) oldalra \(\displaystyle D\)-ben állított merőlegesre is. Ebből következik, hogy \(\displaystyle e\) éppen a háromszög \(\displaystyle P\)-hez tartozó Simson-egyenese, következésképpen \(\displaystyle E\) a \(\displaystyle P\) pont merőleges vetülete az \(\displaystyle AC\) egyenesén – más szóval \(\displaystyle P\) az \(\displaystyle AC\)-re \(\displaystyle E\)-ben állított merőlegesre is illeszkedik.

Statisztika:

54 dolgozat érkezett.
5 pontot kapott:	Al-Hag Máté Amin, Andó Viola, Asztalos Ádám, Balogh Ádám Péter, Bán-Szabó Áron, Baski Bence, Beinschroth Ninett, Beke Csongor, Bencsik Ádám, Biró 424 Ádám, Bognár 171 András Károly, Csonka Illés, Fekete Richárd, Fleiner Zsigmond, Füredi Erik Benjámin, Gábriel Tamás, Geretovszky Anna, Hámori Janka, Hegedűs Dániel, Hervay Bence, Jánosik Áron, Kerekes Boldizsár, Kocsis Anett, Kovács 129 Tamás, Laki Anna, Lazur Zsófia, Lengyel Ádám, Lovas Márton, Mácsai Dániel, Mezey Dorottya, Mohay Lili Veronika, Molnár Lehel, Móra Márton Barnabás, Nádor Benedek, Nagy 551 Levente, Németh Márton, Nguyen Bich Diep, Osztényi József, Reimann Kristóf, Somogyi Dalma, Szabó 991 Kornél, Szűcs 064 Tamás, Terjék András József, Tiderenczl Dániel, Velich Nóra, Wiener Anna.
4 pontot kapott:	Kitschner Bernadett, Molnár-Szabó Vilmos, Móricz Benjámin, Seres-Szabó Márton.
3 pontot kapott:	1 versenyző.
1 pontot kapott:	3 versenyző.

A KöMaL 2019. decemberi matematika feladatai