A B. 5124. feladat (2020. október)

B. 5124. A szabályos négyoldalú gúla alaplapja az $\displaystyle ABCD$ négyzet, $\displaystyle E$ a gúla csúcsa. Az $\displaystyle AB$ és $\displaystyle CE$ kitérő élek normáltranszverzálisának talppontjai az $\displaystyle AB$ szakaszon $\displaystyle P$, a $\displaystyle CE$ szakaszon pedig $\displaystyle Q$. Tudjuk, hogy $\displaystyle Q$ felezi a $\displaystyle CE$ élt. Határozzuk meg az $\displaystyle AP: PB$ arányt, és számítsuk ki az alaplapnak az oldallapokkal bezárt szögét.

(5 pont)

A beküldési határidő 2020. november 10-én LEJÁRT.

Megoldás.

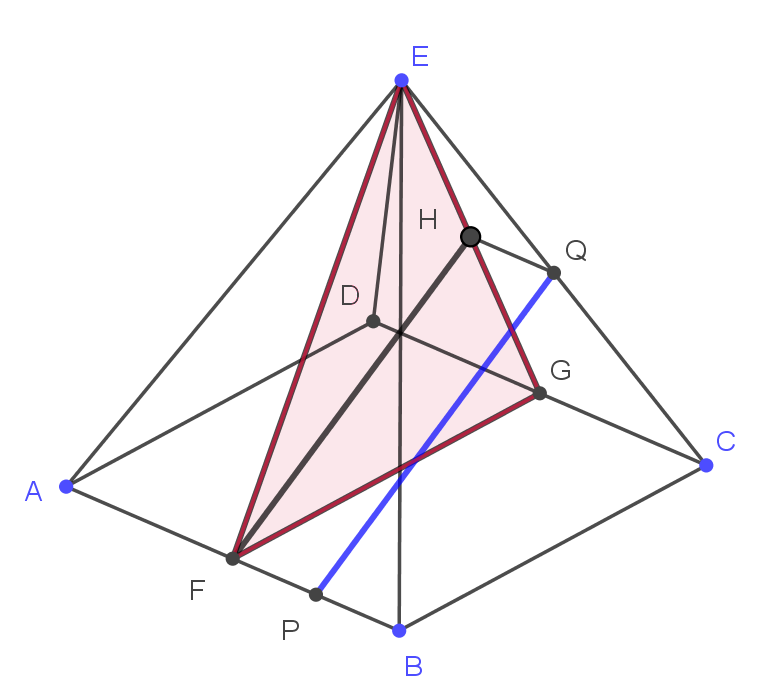
Legyen a gúla $\displaystyle E$ csúcsából az $\displaystyle AB$ élre bocsátott merőleges talppontja $\displaystyle F$, a $\displaystyle CD$ élre bocsátott merőleges talppontja $\displaystyle G$, továbbá az $\displaystyle EG$ oldalmagasságra az $\displaystyle F$ pontból állított merőleges talppontja $\displaystyle H$.

Az $\displaystyle AB$ él párhuzamos a $\displaystyle CD$ éllel, így a $\displaystyle PQ$ normáltranszverzális merőleges a $\displaystyle CD$-re valamint $\displaystyle EC$-re, a $\displaystyle CDE$ lap két nem párhuzamos egyenesére, tehát az egész lapsíkra is. A $\displaystyle DC$ él merőleges az $\displaystyle FGE$ síkra, hiszen $\displaystyle DC\perp FG$ és $\displaystyle DC\perp EG$. Így $\displaystyle FH$, az $\displaystyle EFG$ síkra illeszkedő egyenesként merőleges $\displaystyle DC$-re, valamint $\displaystyle EG$-re, így a $\displaystyle CDE$ síkra is. Mivel ugyanarra a síkra merőlegesek, így $\displaystyle PQ$ és $\displaystyle FH$ párhuzamosak.

Az $\displaystyle AB$ egyenes párhuzamos a $\displaystyle CDE$ síkkal (hiszen annak $\displaystyle CD$ egyenesével is párhuzamos), így minden pontja ugyanaolyan távol van a síktól, így $\displaystyle FH=PQ$, és $\displaystyle FPQH$ téglalap. Így $\displaystyle HQ\parallel FP=AB \parallel GC$, és a párhuzamos szelők tétele miatt $\displaystyle H$ felezi $\displaystyle EG$ szakaszt. Az $\displaystyle EFG$ háromszögben $\displaystyle EF=EG$, hiszen a gúla szabályos. A fentiekben pedig már láttuk, hogy $\displaystyle F$-ből induló magasságvonala felezi a szemközti oldalt, tehát $\displaystyle EF=FG$ is teljesül, az $\displaystyle EFG$ háromszög szabályos. Az $\displaystyle EF$ és $\displaystyle FG$ is merőleges az $\displaystyle AB$ élre, így $\displaystyle EFG\sphericalangle=60^{\circ}$ az alaplap és oldallap hajlásszöge.

Az $\displaystyle EGC$ háromszögben $\displaystyle HQ$ középvonal, tehát $\displaystyle HQ$ és a vele egyenlő hosszúságú $\displaystyle FP$ az alapél negyede. Így azt is tudjuk, hogy a $\displaystyle P$ pont $\displaystyle 3:1$ arányban osztja ketté az $\displaystyle AB$ szakaszt.

Statisztika:

64 dolgozat érkezett.
5 pontot kapott:	Al-Hag Máté Amin, Andó Viola, Bán-Szabó Áron, Baski Bence, Beinschroth Ninett, Bencsik Ádám, Csizmadia Miklós, Csonka Illés, Diaconescu Tashi, Duchon Márton, Egyházi Hanna, Fekete Richárd, Győrffi Ádám György, Hegedűs Dániel, Hervay Bence, Kercsó-Molnár Anita, Kerekes Boldizsár, Koleszár Domonkos, Kovács 129 Tamás, Kökényesi Márk Péter, Lengyel Ádám, Lovas Márton, Lőw László, Mácsai Dániel, Márton Kristóf, Mátéfy Ádám , Móra Márton Barnabás, Nádor Benedek, Nagy 551 Levente, Németh Márton, Nguyen Bich Diep, Nyárfádi Patrik, Osztényi József, Rareș Polenciuc, Révész Máté, Richlik Bence, Romaniuc Albert-Iulian, Seláf Bence, Seres-Szabó Márton, Simon László Bence, Somogyi Dalma, Szakács Ábel, Szeibert Barnabás, Terjék András József, Török Ágoston, Trombitás Karolina Sarolta, Varga Boldizsár, Velich Nóra, Virág Rudolf.
4 pontot kapott:	9 versenyző.
3 pontot kapott:	4 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2020. októberi matematika feladatai