A B. 5127. feladat (2020. november)

B. 5127. Adott egy konvex szögtartomány és egy \(\displaystyle k\) hosszúságú szakasz. Mi a mértani helye azon \(\displaystyle P\) pontoknak a szögtartományban, amelyeken keresztül húzható olyan egyenes, amely éppen \(\displaystyle k\) kerületű háromszöget metsz ki az adott szögtartományból?

(4 pont)

A beküldési határidő 2020. december 10-én LEJÁRT.

Megoldás. Legyen az adott szög csúcsa \(\displaystyle C\), a szögszárak az \(\displaystyle e\) és \(\displaystyle f\) félegyenesek. Vegyünk egy olyan egyenest és ezzel együtt háromszöget, amely megfelel a feladat feltételének. Messe a behúzott egyenes az \(\displaystyle e\) szögszárat az \(\displaystyle A\), az \(\displaystyle f\) szögszárat pedig a \(\displaystyle B\) pontban. Majd rajzoljuk meg az \(\displaystyle ABC\) háromszög \(\displaystyle AB\) oldalához tartozó hozzáírt \(\displaystyle k_C\) kört. Az érintési pontok \(\displaystyle E\), illetve \(\displaystyle F\).

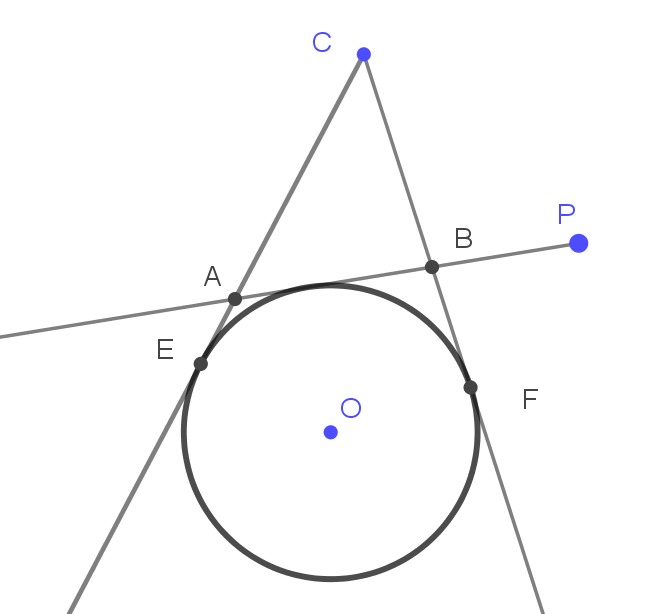
Ismert, hogy a \(\displaystyle k_C\) körnek a \(\displaystyle C\) csúcstól számított \(\displaystyle CE\) és \(\displaystyle CF\) érintőszakaszai a háromszög félkerületével egyenlők. Emiatt az összes megfelelő háromszögnek ugyenez a \(\displaystyle k_C\) kör lesz a \(\displaystyle C\) csúccsal szemközti oldalhoz tartozó hozzáírt köre.

Tudjuk tehát, hogy a megfelelő \(\displaystyle P\) pontok azok, amelyekből ehhez a körhöz olyan érintő is húzható, amely a \(\displaystyle k_C\) körvonalat az \(\displaystyle EF\) íven érinti úgy, hogy elválasztja az \(\displaystyle C\) pontot és az \(\displaystyle EF\) szakaszt. A szögtartomány ezen \(\displaystyle P\) pontjait kell számba vennünk.

A szögtartomány \(\displaystyle EC, CF\) szakaszokkal és \(\displaystyle EF\) körívvel határolt részében a belső pontokra teljesül, hogy azokból mindkét, a körhöz húzott érintő ad egy-egy megoldást, míg a határoló pontok esetében – kivéve az \(\displaystyle E, F, C\) pontokat – minden esetben egy megoldást kapunk.

A körlemez belső pontjai és a szögtartománynak a körön és az előbbi tartományon kívül eső pontjai nem felelnek meg. Ezekből vagy nem húzható érintő a \(\displaystyle k_c\) körhöz, vagy az érintők nem metszik az \(\displaystyle EC\) és \(\displaystyle FC\) szakaszokat.

Statisztika:

63 dolgozat érkezett.
4 pontot kapott:	Angel Ádám, Argay Zsolt, Balogh Ádám Péter, Bán-Szabó Áron, Baski Bence, Bencsik Ádám, Bencsik Dávid, Csizmadia Miklós, Dezső Kende Barnabás, Diaconescu Tashi, Duchon Márton, Farkas 512 Izabella, Fekete Patrik, Fekete Richárd, Hegedűs Dániel, Hervay Bence, Jánosik Máté, Kalocsai Zoltán, Kercsó-Molnár Anita, Kerekes Boldizsár, Koleszár Domonkos, Kovács 129 Tamás, Kökényesi Márk Péter, Köpenczei Csanád, Lengyel Ádám, Lovas Márton, Mácsai Dániel, Mátéfy Ádám , Melján Dávid Gergő, Mohay Lili Veronika, Molnár-Szabó Vilmos, Nádor Benedek, Nagy 551 Levente, Németh Márton, Osztényi József, Páhán Anita Dalma, Rareș Polenciuc, Sándor Péter, Seres-Szabó Márton, Sógor Bence, Somogyi Dalma, Szakács Ábel, Szanyi Attila, Sztranyák Gabriella, Török Ágoston, Varga Boldizsár, Virág Rudolf, Wiener Anna.
3 pontot kapott:	6 versenyző.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	7 versenyző.

A KöMaL 2020. novemberi matematika feladatai