A B. 5144. feladat (2021. január)

B. 5144. Az \(\displaystyle ABCD\) konvex négyszög területe \(\displaystyle t\), egy belső pontja \(\displaystyle O\). Mutassuk meg, hogy

\(\displaystyle 2t\le OA^2+OB^2+OC^2+OD^2. \)

Mikor áll fenn egyenlőség?

(3 pont)

A beküldési határidő 2021. február 15-én LEJÁRT.

Megoldás. Kössük össze az \(\displaystyle O\) belső pontot a csúcsokkal, így a négyszöget négy háromszögre bontottuk fel.

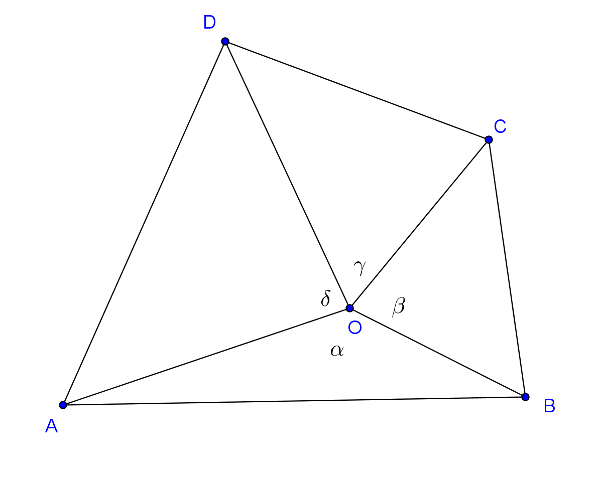
A négyszög területe a négy háromszög területének összege. A háromszögek területét a trigonometrikus területképlettel írjuk fel az ábra szerinti jelölésekkel. Rögtön a kétszeres területre térve nem kell \(\displaystyle 2\)-vel osztanunk az egyes területeknél:

\(\displaystyle 2t=OA\cdot OB\sin\alpha+OB\cdot OC\sin\beta+OC\cdot OD\sin\gamma+OD\cdot OA\sin\delta.\)

A szögek szinusza legfeljebb \(\displaystyle 1\), így azonnal egy felső becslést kapunk, ha mindegyik helyébe \(\displaystyle 1\)-et írunk:

\(\displaystyle 2t\le OA\cdot OB+OB\cdot OC+OC\cdot OD+OD\cdot OA.\)

A számtani- és mértani közép közötti egyenlőtlenség felhasználásával (illetve az ezzel ekvivalens tény alapján, hogy \(\displaystyle (x-y)^2\ge 0\) átrendezésével \(\displaystyle xy\le \frac{x^2+y^2}{2}\)):

\(\displaystyle 2t\le \frac{OA^2+OB^2}{2}+\frac{OB^2+OC^2}{2}+\frac{OC^2+OD^2}{2}+\frac{OD^2+OA^2}{2}=OA^2+OB^2+OC^2+OD^2.\)

Ez a bizonyítandó állítás.

Két helyen alkalmaztunk felső becslést. Az első esetben, a trigonometrikus területképletek után akkor van egyenlőség, ha a szinuszértékek mindegyike pontosan \(\displaystyle 1\), vagyis az \(\displaystyle O\) pont a négyszög egymásra merőleges átlóinak metszéspontja, míg a második esetben, a számtani-mértani középnél akkor, ha a \(\displaystyle OA=OB=OC=OD\), vagyis a két feltétel alapján akkor, ha az \(\displaystyle ABCD\) négyszög négyzet, és \(\displaystyle O\) a középpontja.

Megjegyzés. Az állítás konkáv négyszögre is teljesül. Ha az \(\displaystyle O\) ponttal úgy tudjuk négy háromszögre bontani a négyszöget, mint a konvex esetnél, akkor a bizonyítás azzal teljesen megegyező. Lehetséges viszont, hogy az \(\displaystyle O\) pont úgy helyezkedik el, hogy az egyik csúccsal összekötő szakasz belső pontban metszi az egyik oldalt. Ekkor az ábra szerinti jelölésekkel betűzzünk és essen az \(\displaystyle O\) pont az \(\displaystyle ABC\) háromszög belsejébe, úgy, hogy az \(\displaystyle OD\) szakasz metszi a \(\displaystyle BC\) oldalt.

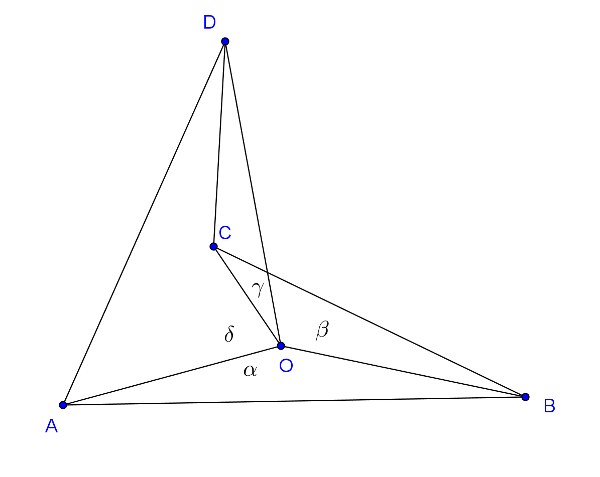
Ekkor A négyszög területét úgy kapjuk, hogy az \(\displaystyle AOB, BOC\) és \(\displaystyle ODA\) háromszögek területének összegéből levonjuk az \(\displaystyle OCD\) háromszög területét. A kétszeres terület kiszámítása így módosul:

\(\displaystyle 2t=OA\cdot OB\sin\alpha+OB\cdot OC\sin\beta-OC\cdot OD\sin\gamma+OD\cdot OA\sin\delta.\)

A felső becslésnél már írhatunk plusz előjelet, és végig igazak maradnak az első esetnél leírtak, kivéve természetesen azt a tényt, hogy itt nem léphet fel egyenlőség.

Statisztika:

95 dolgozat érkezett.
3 pontot kapott:	65 versenyző.
2 pontot kapott:	24 versenyző.
1 pontot kapott:	4 versenyző.
0 pontot kapott:	2 versenyző.

A KöMaL 2021. januári matematika feladatai