 |
A B. 5148. feladat (2021. január) |
B. 5148. Az \(\displaystyle ABC\) háromszögnek \(\displaystyle C\)-nél derékszöge van. A háromszögbe írt kör a \(\displaystyle BC\) befogót a \(\displaystyle D\), az \(\displaystyle AC\) befogót az \(\displaystyle E\) pontban érinti. A \(\displaystyle BC\) oldalhoz hozzáírt kör a \(\displaystyle BC\) szakaszt a \(\displaystyle G\) pontban érinti; hasonlóan, az \(\displaystyle AC\) oldalhoz hozzáírt kör az \(\displaystyle AC\) szakaszt a \(\displaystyle H\) pontban érinti. A \(\displaystyle DH\) és \(\displaystyle EG\) szakaszok metszéspontja \(\displaystyle M\). Mutassuk meg, hogy a \(\displaystyle DGM\) és az \(\displaystyle EHM\) háromszögek köré írt körök \(\displaystyle M\)-től különböző metszéspontja a beírt körre esik.
(6 pont)
A beküldési határidő 2021. február 15-én LEJÁRT.
Megoldás. Az \(\displaystyle ABC\) háromszöget úgy helyezzük el, hogy irányítása pozitív legyen.
Legyenek a háromszög oldalai \(\displaystyle BC=a\), \(\displaystyle CA=b\) és \(\displaystyle AB=c\), a félkerület \(\displaystyle \frac{a+b+c}2=s\). Jól ismert, hogy a beírt és hozzáírt körök érintési szakaszainak hossza \(\displaystyle AH=BG=CD=CE=s-c\), \(\displaystyle AE=CH=s-a\) és \(\displaystyle BD=CG=s-b\). A leghosszabb oldal az \(\displaystyle AB\) átfogó, ezért \(\displaystyle CE=s-c<s-a=CH\) és \(\displaystyle CD=s-c<s-b=CG\), tehát az \(\displaystyle E\) pont a \(\displaystyle CH\) szakasz belsejébe, a \(\displaystyle D\) pont a \(\displaystyle CG\) szakasz belsejébe esik, az \(\displaystyle M\) pont pedig a \(\displaystyle DEHG\) konvex négyszög \(\displaystyle DH\) és \(\displaystyle EG\) átlóinak metszéspontja.
Jelöljük a beírt kör középpontját \(\displaystyle I\)-vel, és legyenek a háromszög hegyesszögei \(\displaystyle CAB\sphericalangle=\alpha\) és \(\displaystyle ABC\sphericalangle=\beta\); Az \(\displaystyle AI\) és \(\displaystyle BI\) szakaszok felezik a két hegyesszöget. Mivel a háromszög derékszögű, \(\displaystyle \alpha+\beta=90^\circ\).
A \(\displaystyle CEID\) négyszög négyzet, mert a \(\displaystyle C,D,E\) csúcsoknál derékszöge van, és \(\displaystyle DI=EI\) a beírt kör sugarai; ezért \(\displaystyle CD=CE=DI=EI\). Az \(\displaystyle AIE\) és \(\displaystyle HDC\) derékszögű háromszögek egybevágók, mert \(\displaystyle AE=HC\) és \(\displaystyle EI=CD\); emiatt \(\displaystyle DHC\sphericalangle=IAE\sphericalangle=\frac\alpha2\). Az \(\displaystyle A\) és \(\displaystyle B\) pontok szerepének felcserélésével ugyanígy látjuk, hogy \(\displaystyle EGC=\frac\beta2\).
A \(\displaystyle CED\) háromszög egyenlő szárú és derékszögű, ezért \(\displaystyle CED\sphericalangle=EDC\sphericalangle=45^\circ\). A \(\displaystyle GDE\) és \(\displaystyle DEH\) háromszögek szögeinek összeszámolásából kapjuk, hogy \(\displaystyle HDE\sphericalangle = DEC\sphericalangle-DHE\sphericalangle = 45^\circ-\frac\alpha2 = \frac\beta2\), és hasonlóan \(\displaystyle GED\sphericalangle=\frac\alpha2\), továbbá a \(\displaystyle DEM\) háromszögből \(\displaystyle GMD\sphericalangle= MDE\sphericalangle+DEM\sphericalangle=\frac{\alpha+\beta}2=45^\circ\).
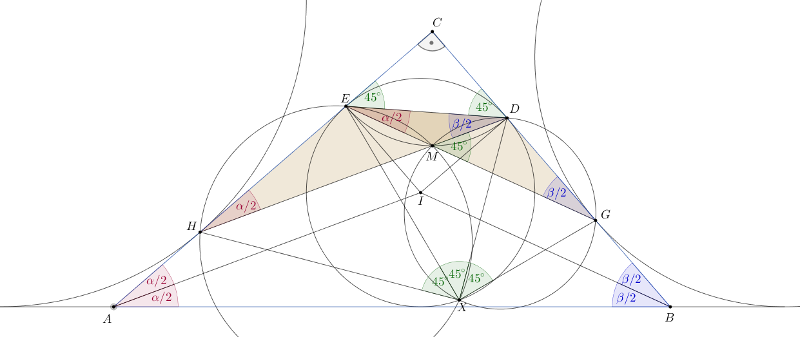
Vegyük észre, hogy a \(\displaystyle GDE\) és \(\displaystyle EHD\) háromszögek hasonlóak, mert szögeik megegyeznek. A két háromszög körüljárása megegyezik, és a megfelelő oldalaik \(\displaystyle 45^\circ\)-os szöget zárnak be egymással, tehát a \(\displaystyle GDE\) háromszög egy \(\displaystyle 45^\circ\)-os, pozitív irányú forgatva nyújtással vihető át a \(\displaystyle DEH\) háromszögbe. Legyen \(\displaystyle X\) ennek a forgatva nyújtásnak a középpontja. Mivel \(\displaystyle G\) képe \(\displaystyle D\), \(\displaystyle D\) képe \(\displaystyle E\) és \(\displaystyle E\) képe \(\displaystyle H\), az \(\displaystyle XGD\), \(\displaystyle XDE\), \(\displaystyle XEH\) háromszögek pozitív körüljárásúak és \(\displaystyle DXG\sphericalangle = EXD\sphericalangle = HXE\sphericalangle = 45^\circ\).
Az \(\displaystyle XGD\) és az \(\displaystyle MGD\) háromszög is pozitív körüljárású, ezért az \(\displaystyle X\) és \(\displaystyle M\) pontok a \(\displaystyle GD\) szakasznak ugyanarra az oldalára esnek; továbbá \(\displaystyle DXG\sphericalangle = DMG\sphericalangle = 45^\circ\), ezért a kerületi szögek tételének megfordítása szerint az \(\displaystyle X\) pont a \(\displaystyle GMD\) köríven van.
Ugyanígy, az \(\displaystyle XEH\) és az \(\displaystyle MEH\) háromszög is pozitív körüljárású és \(\displaystyle HXE\sphericalangle = HME\sphericalangle = 45^\circ\), ezért a \(\displaystyle HME\) körív is átmegy \(\displaystyle X\)-en.
Az \(\displaystyle X\) pont nem eshet egybe az \(\displaystyle M\) ponttal, mert \(\displaystyle EXD\sphericalangle=45^\circ\ne EMD\sphericalangle=135^\circ\). Tehát \(\displaystyle X\) a \(\displaystyle DGM\) és az \(\displaystyle EHM\) körök \(\displaystyle M\)-től különböző metszéspontja.
Végül, az \(\displaystyle XDE\) és az \(\displaystyle IDE\) háromszög is pozitív körüljárású és \(\displaystyle EXD\sphericalangle = \frac12 EID\sphericalangle = 45^\circ\), ezért a kerületi és középponti szögek tételének megfordítása miatt az \(\displaystyle X\) pont a beírt körnek a hosszabbik \(\displaystyle ED\) ívére esik.
Statisztika:
42 dolgozat érkezett. 6 pontot kapott: Balogh Ádám Péter, Bán-Szabó Áron, Bencsik Dávid, Diaconescu Tashi, Kalocsai Zoltán, Metzger Ábris András, Móricz Benjámin, Rareș Polenciuc, Simon László Bence, Somogyi Dalma, Sztranyák Gabriella, Török Ágoston. 5 pontot kapott: Andó Viola, Arató Zita, Baski Bence, Beinschroth Ninett, Csizmadia Miklós, Csonka Illés, Duchon Márton, Fekete Richárd, Győrffi Ádám György, Hegedűs Dániel, Horváth 530 Mihály, Kovács 129 Tamás, Kökényesi Márk Péter, Lenkey Gyöngyvér, Lovas Márton, Mohay Lili Veronika, Molnár-Szabó Vilmos, Nádor Benedek, Nagy 551 Levente, Németh Márton, Osztényi József, Páhán Anita Dalma, Seres-Szabó Márton, Varga Boldizsár, Velich Nóra, Virág Rudolf, Wiener Anna. 0 pontot kapott: 3 versenyző.
A KöMaL 2021. januári matematika feladatai
