A B. 5153. feladat (2021. február)

B. 5153. Legyenek \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) egy egységnyi oldalú szabályos háromszög csúcsai, míg \(\displaystyle D\) egy pont az \(\displaystyle AB\) oldal \(\displaystyle B\)-n túli meghosszabbításán. A \(\displaystyle BC\) szakaszra \(\displaystyle B\)-ben állított merőleges a \(\displaystyle CD\) szakaszt az \(\displaystyle E\) pontban metszi. Határozzuk meg a \(\displaystyle CE\) szakasz hosszát, ha \(\displaystyle ED=1\).

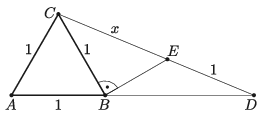
Javasolta: Szilassi Lajos és Tarcsay Tamás (Szeged)

(4 pont)

A beküldési határidő 2021. március 10-én LEJÁRT.

Megoldás. A \(\displaystyle B\) pont \(\displaystyle A\)-ra vonatkozó tükörképét jelölje \(\displaystyle B'\). Legyen továbbá \(\displaystyle x=EC\).

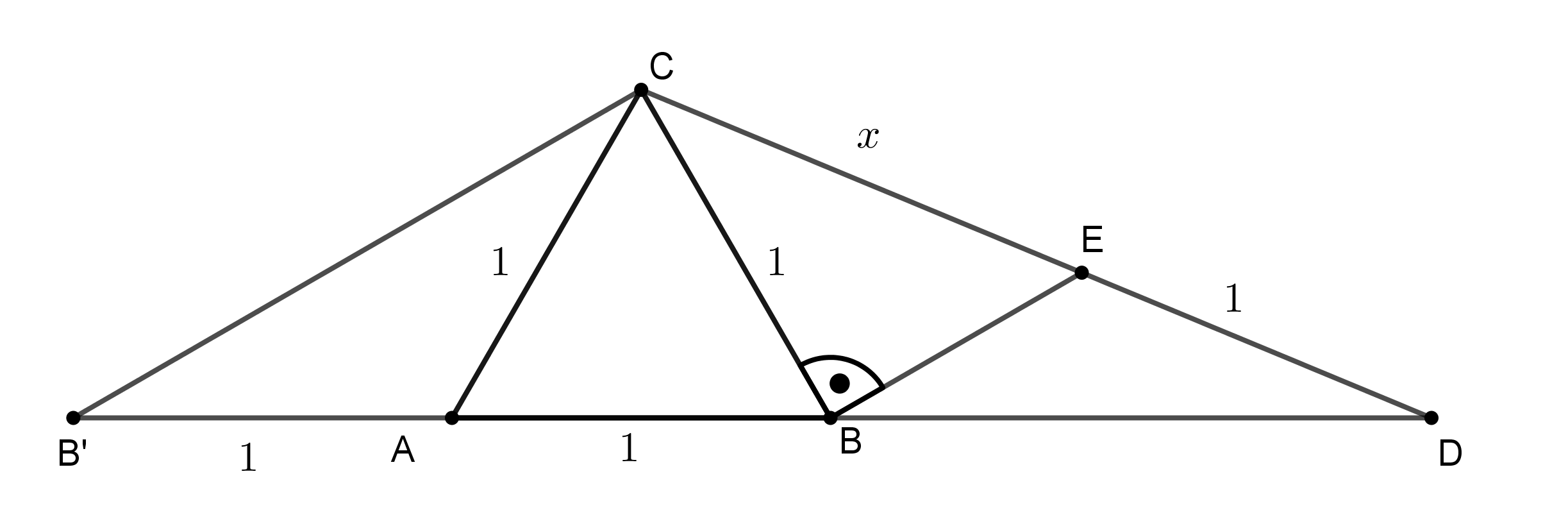
Az \(\displaystyle AB'C\) háromszög egyenlő szárú, \(\displaystyle B'A=AB=AC=1\), \(\displaystyle CB'A\sphericalangle = B'CA\sphericalangle = \frac{1}{2}CAB\sphericalangle = 30^{\circ}\), ezért \(\displaystyle B'C=\sqrt{3}\). Továbbá \(\displaystyle CB'D\sphericalangle = 30^{\circ} = 180^{\circ} - (90^{\circ} + 60^{\circ}) = 180^{\circ} - (EBC\sphericalangle + CBA\sphericalangle) = DBE\sphericalangle\). Így a \(\displaystyle DB'C\) és \(\displaystyle EBD\) háromszögek hasonlók, következésképpen

\(\displaystyle \frac{CB'}{CD} = \frac{EB}{DE}, \)

tehát Pitagorasz tétele és a feladat feltételei alapján

\(\displaystyle \frac{\sqrt{3}}{x+1} = \frac{\sqrt{x^2-1}}{1}. \)

Négyzetre emelve, rendezve, majd szorzattá alakítva:

\(\displaystyle \frac{3}{x^2+2x+1} = \frac{x^2-1}{1}, \)

\(\displaystyle 3 = (x^2+2x+1)(x^2-1), \)

\(\displaystyle 0=x^4 + 2x^3 - 2x -4 = (x+2)(x^3 - 2). \)

A kapott egyenlet egyetlen pozitív megoldása \(\displaystyle EC=x=\root {3}\of {2}\).

Megjegyzés. A feladat kitűzői a probléma matematikatörténeti vonatkozásaira szeretnék felhívni az érdeklődők figyelmét:

Egy KöMaL feladat, és ami mögötte van....
A neuszisz vonalzó

Statisztika:

82 dolgozat érkezett.
4 pontot kapott:	67 versenyző.
3 pontot kapott:	7 versenyző.
2 pontot kapott:	6 versenyző.
1 pontot kapott:	2 versenyző.

A KöMaL 2021. februári matematika feladatai