 |
A B. 5156. feladat (2021. február) |
B. 5156. Legyen \(\displaystyle K\) egy konvex \(\displaystyle 2n\)-szög, amelynek minden oldala egységnyi, és szemközti oldalai párhuzamosak. Mutassuk meg, hogy \(\displaystyle K\)-t fel lehet bontani véges sok egységnyi oldalhosszúságú rombuszra. Hány rombuszból állhat egy ilyen felbontás?
(6 pont)
A beküldési határidő 2021. március 10-én LEJÁRT.
Megoldás. Betűzzük meg \(\displaystyle K\) csúcsait pozitív körüljárás szerint: \(\displaystyle A_1, A_2,..., A_{2n}\). Jelölje továbbá minden \(\displaystyle 3 \leq i \leq n\) esetén a \(\displaystyle A'_i\) az \(\displaystyle A_i\) pontnak az \(\displaystyle \overrightarrow{A_2A_1}\) vektorral való eltoltját. Ekkor az
\(\displaystyle A_1A_2A_3A'_3, \quad A'_3A_3A_4A'_4, \quad \ldots, \quad A'_iA_iA_{i+1}A'_{i+1}, \quad \ldots, \quad A'_{n-1}A_{n-1}A_nA'_n, \quad A'_nA_nA_{n+1}A_{n+2} \)
négyszögek mind rombuszok, összesen \(\displaystyle n-1\) darab.
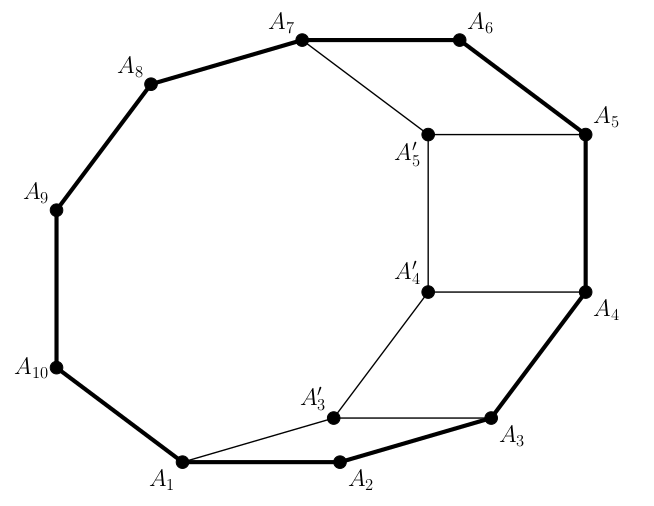
\(\displaystyle K\) előáll mint ezen a rombuszok, illetve az \(\displaystyle A_1 A'_3 A'_4 \ldots A'_n A_{n+2} A_{n+1} \ldots A_{2n}\) konvex \(\displaystyle (2n-2)\)-szög uniója. Erre a \(\displaystyle (2n-2)\)-szögre megismételhetjük az előbbi eljárást, így most \(\displaystyle n-2\) darab rombuszt tudunk leválasztani a sokszögből. Az eljárást tovább ismételgethetjük, amíg az \(\displaystyle (n-2)\)-edik alkalmazása után már csak egy olyan négyszög fog maradni, amely maga is rombusz.
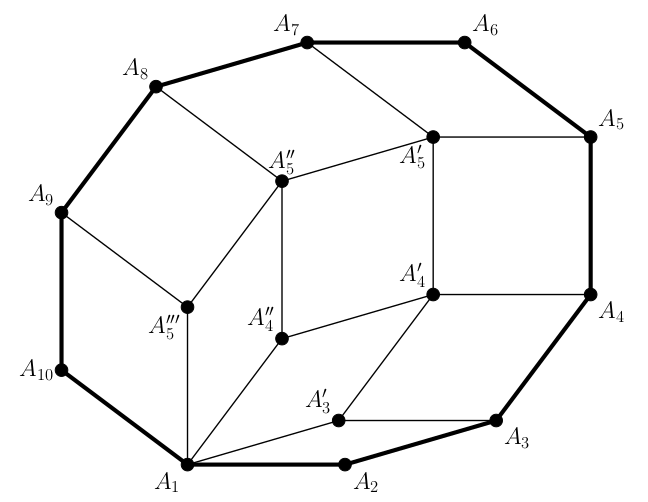
Így a \(\displaystyle 2n\)-szöget felbontottuk
\(\displaystyle (n-1) + (n-2) + \ldots + 1 = \binom{n}{2} \)
darab rombuszra.
Bebizonyítjuk, hogy minden más felbontás is \(\displaystyle \binom{n}{2}\) darab rombuszból kell álljon.
Ehhez először kimondunk egy technikai jellegű lemmát, amelyet majd a megoldás végén külön bizonyítunk. A lemmában és a későbbiekben \(\displaystyle K\)-oldalnak nevezzük a felbontott sokszög külső oldalait.
Technikai Lemma: Egy felbontás minden rombuszának minden olyan oldalához, amely nem \(\displaystyle K\)-oldal, teljes oldalával csatlakozik a felbontás egy másik rombusza.
Legyen \(\displaystyle \mathcal{R}\) egy tetszőleges rombusz a felbontásból, \(\displaystyle \mathcal{R}\) középpontját jelölje \(\displaystyle K\).
Válasszuk ki \(\displaystyle \mathcal{R}\) egy oldalát, ezt jelölje \(\displaystyle r_1\). Ha \(\displaystyle r_1\) nem \(\displaystyle K\)-oldal, akkor a technikai lemma szerint a felbontás egy másik, \(\displaystyle \mathcal{R}_1\) rombuszának is oldala. Ennek \(\displaystyle r_1\)-gyel szemközti \(\displaystyle r_2\) oldalához illeszkedik az \(\displaystyle \mathcal{R}_2\) rombusz, ennek \(\displaystyle r_2\)-vel szemközti \(\displaystyle r_3\) oldalához az \(\displaystyle \mathcal{R}_3\) rombusz stb. Így kapjuk az \(\displaystyle \mathcal{R}_1,\mathcal{R}_2,\ldots\) rombusz-sorozatot. Mivel véges sok rombusz van a felbontásban, előbb-utóbb el kell érnünk egy \(\displaystyle K\)-oldalhoz. (Legyen \(\displaystyle t\) az az index, amelyre \(\displaystyle r_t\) a sokszög oldala.)
Ha \(\displaystyle \mathcal{R}\) középpontját \(\displaystyle P\)-vel jelölöm, míg az \(\displaystyle r_i\) oldal felezőpontját \(\displaystyle F_i\)-vel, akkor a \(\displaystyle P F_1 F_2 \ldots F_t\) töröttvonal összeköti \(\displaystyle P\)-t egy \(\displaystyle K\)-oldallal. Ezzel mellékesen beláttuk azt is, hogy a felbontás minden rombuszának összes oldala párhuzamos valamelyik \(\displaystyle K\)-oldallal.
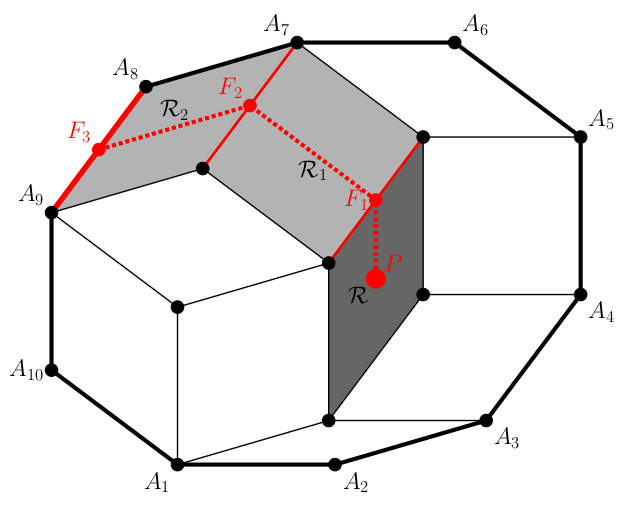
Ha ezt az eljárást az \(\displaystyle \mathcal{R}\) rombusznak az \(\displaystyle r_1\)-gyel szemközti oldalán indítom, akkor persze abban az irányban is eljutok a \(\displaystyle K\) sokszög egy oldalához. Mivel a rombuszok szemközti oldalai párhuzamosak, így éppen az előbb megtalált \(\displaystyle K\)-oldallal párhuzamos (azaz vele átellenes) \(\displaystyle K\)-oldalhoz fogok eljutni. (Persze ezek párhuzamosak \(\displaystyle \mathcal{R}\) megfelelő oldalaival is).
A \(\displaystyle P\)-ből a szemközti oldalfelező-pontokhoz vezetett töröttvonalakat összefűzve egy olyan töröttvonalat kapok, amely \(\displaystyle K\) egy szemközti oldalpárját köti össze. Ezeket a töröttvonalakat szalagoknak fogom nevezni.
Világos, hogy \(\displaystyle \mathcal{R}\) másik szemköztes oldalpárján át is vezethető egy szalag, amely a \(\displaystyle K\)-nak ezekkel párhuzamos oldalpárját köti össze. Sőt, \(\displaystyle K\)-nak bármely szemközti (azaz párhuzamos) oldalpárját kiválasztva összeköti őket egy egyértelmű ilyen szalag (ha az \(\displaystyle \mathcal{R}\)-t a \(\displaystyle K\) egy oldalára illeszkedő rombusznak választom, akkor az megadja ennek az oldalnak és párjának szalagját).
Tehát a rombuszt átszeli \(\displaystyle n\) ilyen szalag. A felbontás minden rombuszának középpontjában két ilyen szalag metszi egymást. Másrészt ahol két szalag szalag metszi egymást, az mindig egy rombusz középpontja.
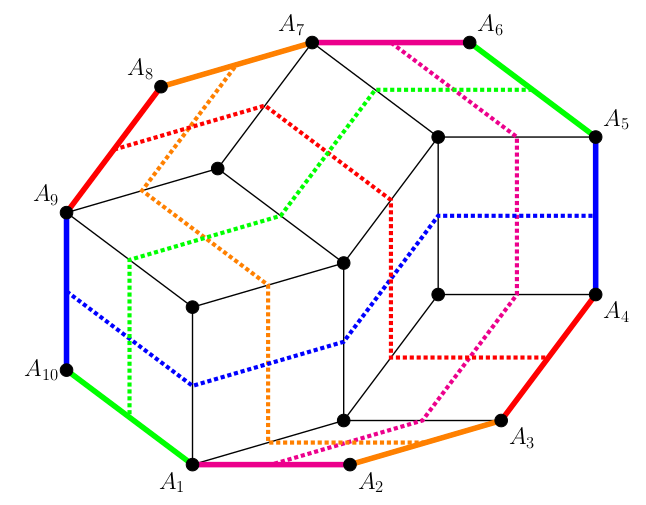
Szalagkereszteződési lemma Bármely két szalag pontosan egy pontban metszi egymást.
Ha ezt a lemmát belátjuk, akkor készen is vagyunk. Hiszen ekkor minden rombusz egyértelműen megfeleltethető egy szalagpárnak. (Szalagpárokból pedig nyilván \(\displaystyle \binom{n}{2}\) van).
Szalagkereszteződési lemma bizonyítása Válasszunk ki kettőt a szalagok közül, az egyiket színezzük ki pirosra, a másikat pedig kékre.
Irányítsuk meg a piros szalagot valamelyik végétől a másik felé. A piros szalag így \(\displaystyle K\)-t kettévágja egy tőle balra és egy tőle jobbara eső tartományra. Mivel a szalagok szemköztes végeket kötnek össze, ezért a kék szalag két vége a piros szalag különböző oldalán van. Emiatt a kék szalag biztosan metszi a piros szalagot legalább egyszer.
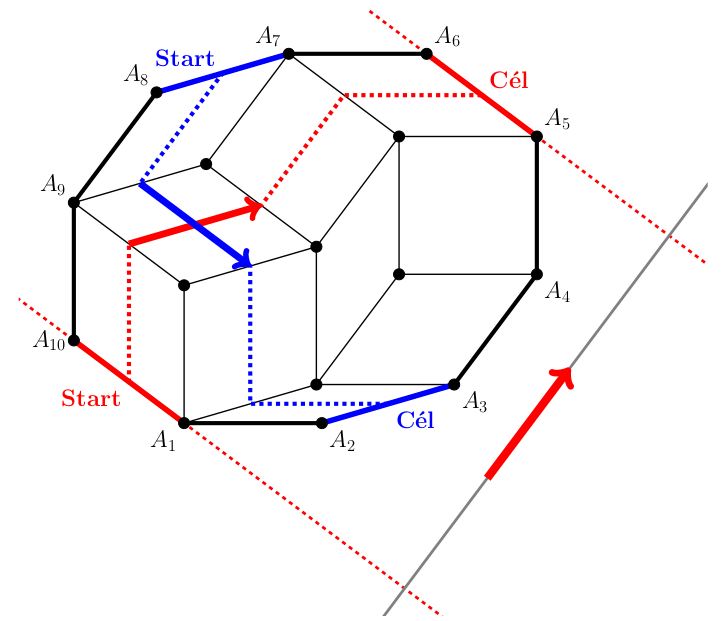
De miért nem metszheti többször? Ennek belátásához irányítsuk meg a kék szalagot úgy, hogy a piros szalag bal oldaláról induljon és a jobb oldalára érkezzen. Így amikor a kék szalag először eléri a piros szalagot, akkor balról jobbra kell átmetszenie. Ha a kék szakaszon továbbmenve lenne egy második találkozás, akkor ott jobbról balra kellene metszenie a piros szalagot. De mindjárt belátjuk, hogy a kék szalag nem tudja jobbról balra metszeni a pirosat.
Ehhez értsük meg kicsit jobban az irányított szalagokat. A szalag \(\displaystyle K\) két szemközti oldalát köti össze. Ahonnan indul, azt nevezzük a szalag startvonalának, ahova érkezik, azt nevezzük a célvonalának. Hosszabbítsuk meg a start és a célvonalat egyenessé.
Vegyük észre, hogy ha a piros szalagon végigmegyünk a starttól a célig, akkor végig távolodunk a startvonal egyenesétől, de közeledünk a célvonal egyeneséhez.
Vegyünk egy tetszőleges rombuszt, amelyen a piros szalag áthalad. Ennek a rombusznak két oldala párhuzamos a piros szalag start és célvonalával. Ezek felezőpontjai között két ellentétes irányban mehetne a szalag, de a kétféle irány közül pontosan az egyikre teljesül az, hogy távolodunk a startvonal egyenesétől és közeledünk a célvonal egyeneséhez. Ugyanígy persze a kék szalag irányát is egyértelműen meg tudjuk mondani minden általa érintett rombuszon belül.
Ha lenne több rombusz is, amelyeken belül a kék és a piros szalag találkozik, ezek ugyanolyan állásúak lennének, és így ugyanolyan irányba kellene bennük mutasson a piros és a kék szalag irányítása. De ez azt jelenti, hogy ha az egyik rombuszban balról jobbra metsz a kék, akkor a másikban is.
Ha lenne második metszéspont, ott ellentétes irányban kellene a kék szalagnak metszenie a pirosat. Következésképpen nincs második metszéspont. Ezzel bebizonyítottuk a szalagkeresztezési lemmát.
A ,,Technikai lemma'' bizonyítása: Legyen \(\displaystyle ABCD\) a felbontás egyik rombusza és \(\displaystyle AB\) ennek egy olyan oldala, amely nem \(\displaystyle K\)-oldal. Azt kell belátnunk, hogy az \(\displaystyle AB\) oldalhoz egy másik rombusz is teljes oldalával csatlakozik.
Mivel \(\displaystyle K\) konvex, ezért nem lehet, hogy egy rombuszoldalnak egy része \(\displaystyle K\)-oldal, míg egy másik részéhez rombusz csatlakozik. Mivel mindegyik rombuszoldal egységnyi hosszú, ezért egy rombuszoldal legfeljebb két másik rombuszoldallal csatlakozhat.
Így ha az \(\displaystyle ABCD\) rombusz \(\displaystyle AB\) oldalára nem teljesülne a lemma állítása (azaz nem csatlakozna hozzá egy másik rombusz teljes oldalával), akkor két rombuszoldallal kellene találkoznia. Indirekten tegyük fel, hogy ez a helyzet.
Használjuk az ábra jelöléseit (lehetséges, hogy \(\displaystyle I=F\), azaz a két világosszürke rombusz is rendelkezik egy közös oldallal).
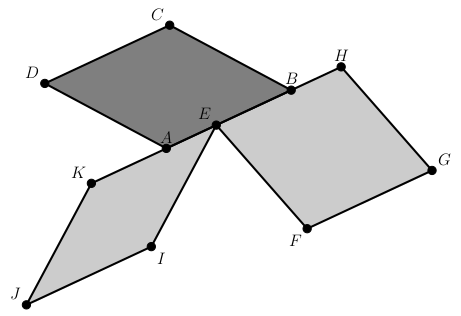
Ekkor \(\displaystyle BH\) szakaszhoz is kell egy \(\displaystyle BB_1\) rombuszoldalnak illeszkednie, ennek \(\displaystyle H\) belső pontja. De ezt a gondolatot továbbvive a sík végtelen sok pontjára tudjuk belátni, hogy valamelyik rombusznak csúcsa.
Legyen minden \(\displaystyle k\) pozitív egészre \(\displaystyle B_k\) illetve \(\displaystyle H_k\) az \(\displaystyle C\) ill. \(\displaystyle H\) pont \(\displaystyle k \cdot \overrightarrow{AB} = k \cdot \overrightarrow{EH}\) vektorral való eltoltja.
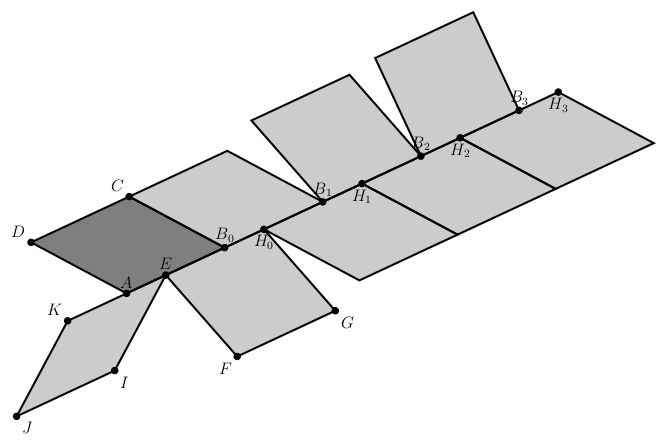
Rekurzív módon minden \(\displaystyle k \geq 0\) egészre beláthatjuk, hogy \(\displaystyle B_k\) és \(\displaystyle H_k\) egy rombusz csúcsa, hiszen:
- Ha \(\displaystyle B_kB_{k+1}\) egy rombuszoldal a belsejében \(\displaystyle H_k\) ponttal,
- akkor \(\displaystyle H_kB_{k+1}\) szakaszhoz is illeszkednie kell egy másik \(\displaystyle H_kH_{k+1}\) rombuszoldalnak, ennek \(\displaystyle B_{k+1}\) belső pontja.
- Most viszont \(\displaystyle B_{k+1}H_k\)-nak kell illeszkednie egy másik \(\displaystyle B_{k+1}B_{k+2}\) rombuszoldalhoz, amelynek \(\displaystyle H_{k+1}\) lesz belső pontja.
Mivel véges sok paralelogrammánk van, csúcsból is csak véges sok lehetne. Azaz ellentmondáshoz jutottunk, tehát az \(\displaystyle AB\) oldal tényleg csak egy másik rombuszoldallal csatlakozhat.
Statisztika:
49 dolgozat érkezett. 6 pontot kapott: Kercsó-Molnár Anita, Kovács 129 Tamás, Kökényesi Márk Péter, Nádor Benedek, Varga Boldizsár, Virág Rudolf. 5 pontot kapott: Bán-Szabó Áron, Ben Gillott, Bencsik Ádám, Bencsik Dávid, Csizmadia Miklós, Duchon Márton, Hegedűs Dániel, Kalocsai Zoltán, Lovas Márton, Németh Márton, Seres-Szabó Márton, Sztranyák Gabriella. 4 pontot kapott: 6 versenyző. 3 pontot kapott: 6 versenyző. 2 pontot kapott: 15 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2021. februári matematika feladatai
