A B. 5277. feladat (2022. november)

B. 5277. Az $\displaystyle ABC$ háromszögbe írt kör középpontja $\displaystyle I$. A $\displaystyle BCA$ körív felezőpontja $\displaystyle F$, az $\displaystyle FI$ egyenes a körülírt kört másodszor az $\displaystyle M$ pontban metszi. Mutassuk meg, hogy a $\displaystyle CM$ egyenes átmegy a beírt és a körülírt kör külső hasonlósági pontján.

Javasolta: Kós Géza (Budapest)

(6 pont)

A beküldési határidő 2022. december 12-én LEJÁRT.

1. megoldás:

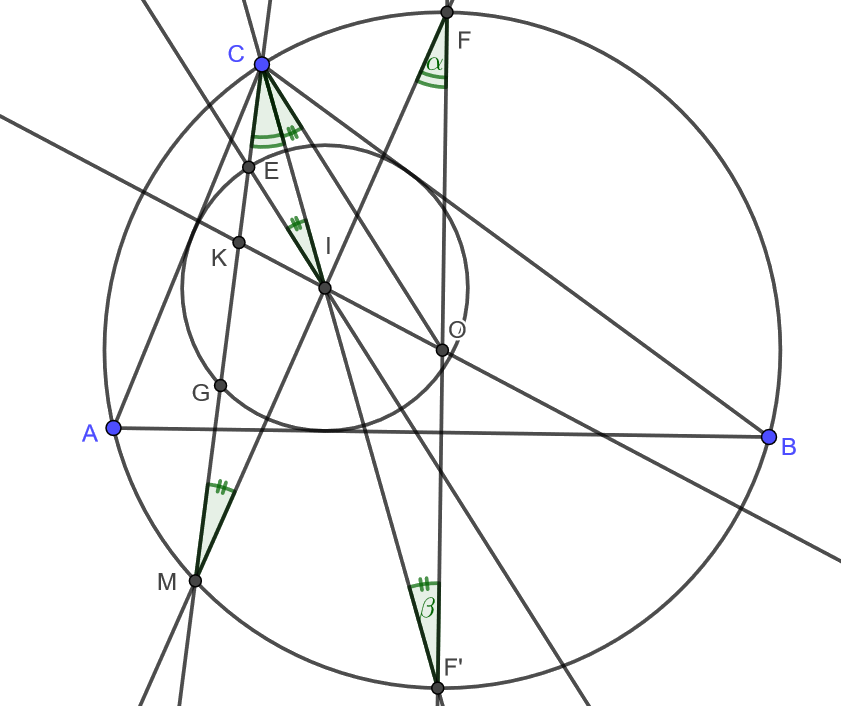
Használjuk az ábra jelöléseit: az általánosság megszorítása nélkül feltehetjük, hogy $\displaystyle AC\le BC$; jelölje $\displaystyle K$ az $\displaystyle MC$ és az $\displaystyle OI$ egyenesek metszéspontját, legyenek $\displaystyle E$ és $\displaystyle G$ a $\displaystyle CM$ egyenes és a beírt kör metszéspontjai, végül $\displaystyle F'$ jelöli a körülírt körön az $\displaystyle F$-fel átellenes pontot, azaz a $\displaystyle C$-t nem tartalmazó $\displaystyle AB$ ív felezőpontját. A beírt kör sugarát $\displaystyle r$, a körülírt körét pedig $\displaystyle R$ jelöli; utóbbiról az általánosság megszorítása nélkül feltehetjük, hogy egységnyi, azaz $\displaystyle R=1$.

A $\displaystyle C$-ből induló belső szögfelezőre a $\displaystyle C$, $\displaystyle I$ és $\displaystyle F'$ pontok mindegyike illeszkedik, ezért $\displaystyle C$, $\displaystyle I$ és $\displaystyle F'$ kollineárisak. Azonos íveken nyugvó kerületi szögek, ezért $\displaystyle MCF'\sphericalangle=MFF'\sphericalangle$ és $\displaystyle CMF\sphericalangle=CF'F \sphericalangle$; ezekre rendre bevezetjük az $\displaystyle \alpha$ és $\displaystyle \beta$ jelölést. A szögek egyenlősége miatt az $\displaystyle MIC$ és $\displaystyle FIF'$ háromszögek hasonlóak, a következőkben trigonometrikus számolásokkal kiszámítjuk az oldalaikat.

Az $\displaystyle FIF'\sphericalangle=180^\circ -\alpha - \beta$, és így az $\displaystyle FIF'$ háromszögre felírt szinusz-tételből

$\displaystyle IF=\frac{2 \sin \beta}{\sin(\alpha+\beta)}, \qquad \text{valamint} \qquad IF'=\frac{2\sin \alpha}{\sin(\alpha +\beta)}.$

A $\displaystyle CM$ szakasz kiszámításához tekintsük a $\displaystyle CMO$ egyenlő szárú háromszöget. A középponti és kerületi szögek tétele szerint $\displaystyle MOF'\sphericalangle=2\alpha$ és $\displaystyle COF\sphericalangle=2\beta$, így az $\displaystyle MOC\sphericalangle$ szárszögre $\displaystyle MOC\sphericalangle=180^\circ - 2\alpha-2\beta$ adódik. Ebből és a szárak egységnyi hosszából $\displaystyle MC=2\sin(90^\circ-\alpha-\beta)=2\cos (\alpha+\beta)$ következik, vagyis az $\displaystyle MIC$ és $\displaystyle FIF'$ háromszögek hasonlóságának aránya $\displaystyle \lambda=MC/FF'=\cos(\alpha+\beta)$. Innen

$\displaystyle CI=\lambda \cdot FI=\frac{2 \sin \beta\cos (\alpha+\beta)}{\sin(\alpha+\beta)}=2\sin \beta \, \ctg(\alpha+\beta), \; \text{valamint} \; MI=\lambda \cdot IF'=\frac{2\sin \alpha \cos (\alpha+\beta)}{\sin(\alpha +\beta)}=2\sin \alpha \, \ctg(\alpha+\beta).$

A következő lépésben kifejezzük $\displaystyle \alpha$ és $\displaystyle \beta$ segítségével $\displaystyle r$-t. Ehhez felírjuk kétféleképpen az $\displaystyle OI^2$ mennyiséget. Egyrészt az Euler-féle összefüggés szerint $\displaystyle OI^2=R^2-2Rr=1-2r$. Másrészről vegyük észre, hogy az $\displaystyle FIF'$ háromszögben $\displaystyle OI$ súlyvonal, így az ismert formula szerint kifejezhetjük a háromszög oldalaiból:

$\displaystyle OI^2=\frac{2F'I^2+2FI^2-F'F^2}{4}=\frac{\frac{8\sin^2 \alpha}{\sin^2(\alpha+\beta)}+\frac{8\sin^2 \beta}{\sin^2(\alpha+\beta)}-4}{4}=\frac{2(\sin^2\alpha+\sin^2 \beta)}{\sin^2(\alpha+\beta)}-1.$

Ezeket összevetve kapjuk, hogy

$\displaystyle r=1-\frac{\sin^2\alpha+\sin^2 \beta}{\sin^2(\alpha+\beta)}=\frac{\sin^2(\alpha+\beta)-\sin^2\alpha-\sin^2 \beta}{\sin^2(\alpha+\beta)}.$

Eddigi számítsaink eredményeit használva, valamint az addíciós formulák szerint

$$\begin{align*}\frac{EI}{CI}=\frac{r}{CI}=\frac{\frac{\sin^2(\alpha+\beta)-\sin^2\alpha-\sin^2 \beta}{\sin^2(\alpha+\beta)}}{2 \sin \beta \, \ctg(\alpha+\beta)}=\frac{\sin^2(\alpha+\beta)-\sin^2\alpha-\sin^2 \beta}{2\sin \beta \cos(\alpha+\beta)}\cdot \frac{1}{\sin(\alpha+\beta)}=\\ =\frac{\sin^2\alpha \cos^2 \beta - \sin^2\alpha + \cos^2\alpha \sin^2\beta - \sin^2 \beta+ 2 \sin \alpha \sin \beta \cos \alpha \cos \beta}{2\sin \beta (\cos \alpha \cos \beta - \sin \alpha \sin \beta)}\cdot \frac{1}{\sin(\alpha+\beta)}=\\ =\frac{-2\sin^2 \alpha \sin^2\beta + 2 \sin \alpha \sin \beta \cos \alpha \cos \beta}{2\sin \beta (\cos \alpha \cos \beta - \sin \alpha \sin \beta)}\cdot \frac{1}{\sin(\alpha+\beta)}=\frac{\sin \alpha}{\sin(\alpha+\beta)}=\frac{F'I}{F'F}. \end{align*}$$

Kaptuk, hogy az $\displaystyle EIC$ és az $\displaystyle F'IF$ háromszögekben két-két oldal aránya megegyezik, továbbá már korábban igazoltuk, hogy van két egyenlő szögük is. Ahhoz, hogy a háromszögek hasonlóságára következtessünk, belátjuk, hogy az $\displaystyle E$-nél, ill. $\displaystyle I$-nél lévő szögeik tompák. A beírt kör középpontja a körülírt körön belül van, azaz $\displaystyle I$ belül van $\displaystyle FF'$ Thalész-körén, így $\displaystyle FIF'\sphericalangle$ tompaszög. Másrészt $\displaystyle GEI\sphericalangle$ a $\displaystyle GEI$ egyenlő szárú háromszög egy alapon fekvő szöge, így szükségképpen hegyesszög, következésképp $\displaystyle CEI\sphericalangle$ kiegészítő szöge tompa. Kaptuk tehát, hogy $\displaystyle CEI\triangle \sim FIF'\triangle$ és így $\displaystyle EIC\sphericalangle=\beta$.

Itt jegyezzük meg, hogy az $\displaystyle IF'O$ háromszögben $\displaystyle R=OF'>IO=r$ miatt $\displaystyle \beta=IF'O\sphericalangle<F'IO\sphericalangle=KIC\sphericalangle$, így a $\displaystyle K$, $\displaystyle E$ és $\displaystyle C$ pontok az $\displaystyle MC$ egyenesen ebben sorrendben követik egymást, azaz az ábránk helyes.

Mivel a $\displaystyle COF'$ háromszög egyenlő szárú, azért $\displaystyle F'CO\sphericalangle=\beta$, és így $\displaystyle EIC\sphericalangle=ICO\sphericalangle$, amiből $\displaystyle EI\parallel CO$. A párhuzamos szelőszakaszok tételét alkalmazva $\displaystyle CKO\sphericalangle$-ben kapjuk, hogy $\displaystyle KI\colon KO=EI \colon CO=r\colon R$, következésképp a $\displaystyle K$ középpontú, $\displaystyle \mu=R/r$ arányú középpontos nagyítás a beírt kört éppen a körülírt körbe képezi. Ez igazolja az állítást.

Diszkusszió: Ha $\displaystyle AC=BC$, akkor $\displaystyle F=C$, az ábra szimmetrikus, $\displaystyle O$ (és $\displaystyle I$) illeszkedik az $\displaystyle FM=CM$ egyenesre, és az állítás nyilvánvaló.

A bizonyítás során használt $\displaystyle G$ és $\displaystyle E$ pontok nem jönnek létre, ha az $\displaystyle M$ pont az $\displaystyle ACB$ körívre esik. Ez azonban nem történhet meg, mert az $\displaystyle AI$ belső szögfelező a körülírt kört az $\displaystyle A$-t nem tartalmazó $\displaystyle BC$ ív felezőpontjában metszi, ami $\displaystyle AC<BC$ feltevésünk mellett elválasztja $\displaystyle F$ és $\displaystyle B$ pontokat.

2. megoldás: Legyen $\displaystyle k$ a körülírt kör, $\displaystyle b$ a beírt kör, és $\displaystyle m$ az a kör, ami érinti az $\displaystyle AC$ és a $\displaystyle BC$ szakaszt, valamint belülről érinti $\displaystyle k$-t. (Angol nyelvterületen "mixtilinear incircle"-nek hívják.) Megmutatjuk, hogy $\displaystyle k$ és $\displaystyle m$ érintési pontja éppen az $\displaystyle M$ pont. Ebből a feladat állítása következik: a Monge-tétel miatt a három kör páronként vett hasonlósági pontjai egy egyenesre esnek, márpedig $\displaystyle b$ és $\displaystyle m$ külső hasonlósági pontja $\displaystyle C$, $\displaystyle k$ és $\displaystyle m$ külső hasonlósági pontja $\displaystyle M$, tehát a Monge-tétel szerint $\displaystyle k$ és $\displaystyle b$ külső hasonlósági pontja is a $\displaystyle CM$ egyenesen van.

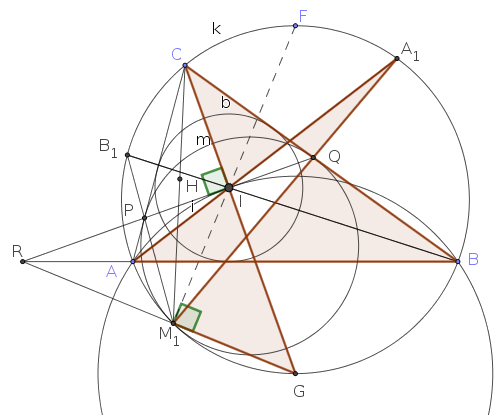
Legyen $\displaystyle m$ érintési pontja a $\displaystyle CA$ szakaszon $\displaystyle P$, a $\displaystyle BC$ szakaszon $\displaystyle Q$, az $\displaystyle AB$ köríven $\displaystyle M_1$, tehát $\displaystyle m$ és $\displaystyle k$ külső hasonlósági pontja $\displaystyle M_1$ (egyelőre még nem bizonyítottuk, hogy $\displaystyle M_1=M$). Legyen az $\displaystyle A$-ból, illetve $\displaystyle B$-ből induló szögfelező és $\displaystyle k$ metszéspontja $\displaystyle A_1$ és $\displaystyle B_1$, ezek felezik a $\displaystyle k$ kör $\displaystyle BC$, illetve $\displaystyle CA$ íveit, és a $\displaystyle k$-hoz $\displaystyle A_1$-ben, illetve $\displaystyle B_1$-ben húzott érintők párhuzamosak a $\displaystyle BC$, illetve a $\displaystyle CA$ szakasszal. Az az $\displaystyle M_1$ középpontú nagyítás, amely $\displaystyle m$-et $\displaystyle k$-ba viszi, a $\displaystyle P$, $\displaystyle Q$ pontokat a $\displaystyle B_1$, $\displaystyle A_1$ pontokba viszi; ezért $\displaystyle M_1$, $\displaystyle P$, $\displaystyle B_1$, illetve $\displaystyle M_1$, $\displaystyle Q$, $\displaystyle A_1$ egy egyenesen van.

Írjuk fel a Pascal-tételt az $\displaystyle ACBB_1M_1A_1$ hatszögre: azt kapjuk, hogy $\displaystyle AC\cap B_1M_1=P$, $\displaystyle CB\cap M_1A_1=Q$ és $\displaystyle BB_1\cap A_1A=I$ egy egyenesen van. Mivel $\displaystyle CP=CQ$ az $\displaystyle m$-hez $\displaystyle C$-ből húzott érintők, $\displaystyle CI$ a $\displaystyle CPQ$ egyenlő szárú háromszög magassága, így $\displaystyle CI\perp PQ$.

Legyen most $\displaystyle G$ az $\displaystyle AB$ körív felezőpontja; ezen átmegy a $\displaystyle CI$ szögfelező, és legyen $\displaystyle R$ az $\displaystyle AB$ és a $\displaystyle GM_1$ egyenesek metszéspontja. Ha a Pascal-tételt az $\displaystyle ABCGM_1A_1$ hatszögre írjuk fel, látjuk, hogy $\displaystyle AB\cap GM_1=R$, $\displaystyle BC\cap M_1A_1=Q$ és $\displaystyle CG\cap A_1A=I$ egy egyenesen van, tehát a $\displaystyle PIQ$ egyenes átmegy az $\displaystyle R$ ponton.

Jól ismert, hogy a beírt kör $\displaystyle I$ középpontja a $\displaystyle G$ középpontú, $\displaystyle A,B$-n átmenő körön van; a $\displaystyle PIQR$ egyenes érinti az $\displaystyle ABI$ kört, mert merőleges a kör $\displaystyle GI$ sugarára. A $\displaystyle R$ pontnak az $\displaystyle ABI$ és a $\displaystyle k$ körre való hatványából

$\displaystyle RI^2 = RA\cdot RB = RM_1\cdot RG, $

ebből következik, hogy $\displaystyle RIM_1\triangle\sim RGI\triangle$, ezért $\displaystyle IM_1R\angle=GIR\angle=90^\circ$.

A Thalész-tétel miatt az $\displaystyle M_1I$ egyenes átmegy a $\displaystyle k$-nak a $\displaystyle G$-vel átellenes pontján, ami az $\displaystyle F$ pont. Tehát $\displaystyle M_1$, $\displaystyle I$ és $\displaystyle F$ egy egyenesen van, és ez bizonyítja, hogy $\displaystyle M_1=M$.

Statisztika:

15 dolgozat érkezett.

6 pontot kapott: Bodor Mátyás, Diaconescu Tashi, Elekes Dorottya, Fülöp Csilla, Lovas Márton, Simon László Bence, Tarján Bernát, Varga Boldizsár, Virág Rudolf, Wiener Anna, Zömbik Barnabás.

5 pontot kapott: Chrobák Gergő, Ho Tran Khanh Linh.

1 pontot kapott: 2 versenyző.

A KöMaL 2022. novemberi matematika feladatai

15 dolgozat érkezett.
6 pontot kapott:	Bodor Mátyás, Diaconescu Tashi, Elekes Dorottya, Fülöp Csilla, Lovas Márton, Simon László Bence, Tarján Bernát, Varga Boldizsár, Virág Rudolf, Wiener Anna, Zömbik Barnabás.
5 pontot kapott:	Chrobák Gergő, Ho Tran Khanh Linh.
1 pontot kapott:	2 versenyző.

Már regisztráltál?
Új vendég vagy?