 |
A B. 5283. feladat (2022. december) |
B. 5283. Az \(\displaystyle N\) konvex négyszög tartalmaz egy \(\displaystyle r\) sugarú körlapot. Mutassuk meg, hogy \(\displaystyle N\) kerülete legalább \(\displaystyle 8r\).
Javasolta: Vígh Viktor (Sándorfalva)
(4 pont)
A beküldési határidő 2023. január 10-én LEJÁRT.
Megoldás. Jelölje a körlapot \(\displaystyle k\), a kerületet pedig \(\displaystyle K(\cdot)\). Toljuk el a kör középpontja felé párhuzamosan az \(\displaystyle N\) oldalegyeneseit úgy, hogy érintsék \(\displaystyle k\)-t, így kapjuk az \(\displaystyle N'\) négyszöget (lásd ábra). Ismert, hogy konvex síkidomok esetén a kerület a tartalmazásra nézve monoton, azaz ha \(\displaystyle L_1\supseteq L_2\) konvex lemezek, akkor \(\displaystyle K(L_1)\ge K(L_2)\). Ebből adódóan \(\displaystyle K(N)\ge K(N')\), és elég az állítást \(\displaystyle N'\)-re igazolni.
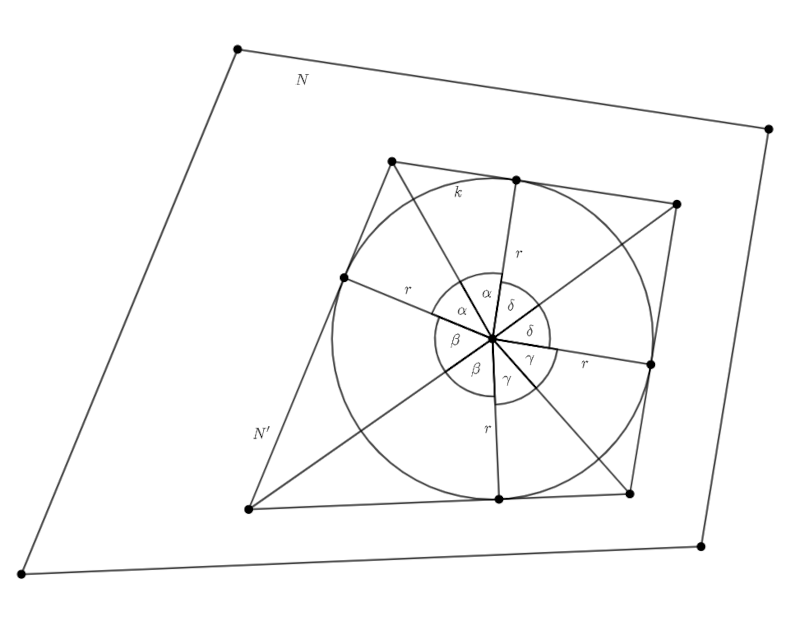
Kössük össze \(\displaystyle k\) középpontját \(\displaystyle N'\) csúcsaival, ill. az oldalakon keletkező érintési pontokkal. Így a középpontnál lévő teljes szöget nyolc hegyesszögre osztottuk, melyek páronként egyenlőek, jelöljük ezeket az ábra szerint. Nyilvánvalóan \(\displaystyle \alpha+\beta+\gamma+\delta=\pi\), továbbá a tangens szögfüggvény definíciója szerint \(\displaystyle K(N')=2r(\tg \alpha+\tg \beta +\tg \gamma + \tg \delta)\).
Mivel a tangens függvény a \(\displaystyle [0, \pi/2)\) intervallumon (szigorúan) konvex, így a Jensen-egyenlőtlenség szerint
\(\displaystyle \frac {\tg \alpha+\tg \beta +\tg \gamma + \tg \delta}4\ge \tg \left ( \frac {\alpha+\beta+\gamma+\delta}{4}\right )=\tg \frac \pi 4=1.\)
Az eddigiekből
\(\displaystyle K(N)\ge K(N')=2r(\tg \alpha+\tg \beta +\tg \gamma + \tg \delta)\ge 2r\cdot 4=8r,\)
amivel az állítást beláttuk.
Egyenlőség akkor áll, ha \(\displaystyle N=N'\) és \(\displaystyle \alpha=\beta=\gamma=\delta=\pi/4\), azaz ha \(\displaystyle N\) négyzet és \(\displaystyle k\) a beírt köre.
Statisztika:
84 dolgozat érkezett. 4 pontot kapott: Ali Richárd, Aravin Peter, Bencz Benedek, Bettesch Helga Adél, Bodor Mátyás, Christ Miranda Anna, Chrobák Gergő, Csonka Illés, Csupor Albert Dezső, Czanik Pál, Czirják Márton Pál, Dávid Dániel, Diaconescu Tashi, Domján Olivér, Fekete Martin, Fórizs Emma, Fülöp Csilla, Guthy Gábor, Kerekes András, Kosztolányi Karina, Kovács Benedek Noel, László Anna, Mizik Lóránt, Nguyen Kim Dorka, Petrányi Lilla, Romaniuc Albert-Iulian, Simon László Bence, Sütő Áron, Szabó 810 Levente, Szakács Ábel, Szakács Domonkos, Szanyi Attila, Tarján Bernát, Török Eszter Júlia, Tusnády Sámuel, Varga Boldizsár, Virág Lénárd Dániel, Wiener Anna, Zhai Yu Fan, Zömbik Barnabás. 3 pontot kapott: 14 versenyző. 2 pontot kapott: 11 versenyző. 1 pontot kapott: 6 versenyző. 0 pontot kapott: 8 versenyző. Nem versenyszerű: 3 dolgozat.
A KöMaL 2022. decemberi matematika feladatai
