 |
A B. 5292. feladat (2023. január) |
B. 5292. Adott egy \(\displaystyle k\) kör és a belsejében a \(\displaystyle P\) és a \(\displaystyle Q\) pontok. Szerkesszünk (írjuk le a szerkesztés menetét – az elemi szerkesztési lépéseket, mint pl. szög felezése, tengelyes tükrözés, nem kell részletezni – és indokoljuk az eljárás helyességét; magát a szerkesztést nem kell papíron elvégezni) a \(\displaystyle P\) és \(\displaystyle Q\) pontokon át olyan kört, amely a \(\displaystyle k\) kört két átellenes pontjában metszi. A \(\displaystyle P\) és \(\displaystyle Q\) pontok helyzetétől függően hány megoldása van a feladatnak?
Javasolta: Kató Gábor (Kápolnásnyék)
(5 pont)
A beküldési határidő 2023. február 10-én LEJÁRT.
Megoldás. Induljunk ki a megoldásból, a \(\displaystyle k\) kör középpontja legyen \(\displaystyle O\), a keresett körvonal legyen \(\displaystyle \kappa\), és jelölje \(\displaystyle X\) és \(\displaystyle Y\) az átmérő két végpontját. A \(\displaystyle PQ\) és \(\displaystyle XY\) egyenesek metszéspontja legyen \(\displaystyle M\).
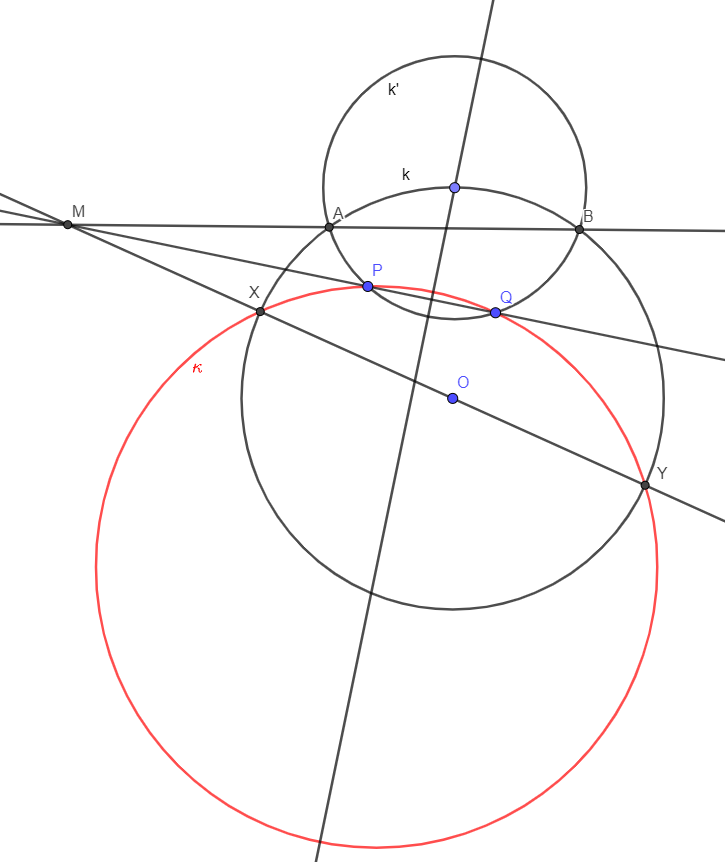
Az \(\displaystyle M\) pont \(\displaystyle \kappa\) körre vonatkozó hatványa \(\displaystyle MP\cdot MQ=MX\cdot MY\), ahol előjeles hosszokkal számolunk, azaz az \(\displaystyle MP\cdot MQ\) szorzat negatív, ha \(\displaystyle M\) a \(\displaystyle PQ\) szakasz belső pontja, és pozitív egyébként (\(\displaystyle XY\)-ra hasonlóan). Vagyis \(\displaystyle M\) a \(\displaystyle PQ\) egyenes olyan pontja, amelynek \(\displaystyle k\)-ra vonatkozó hatványa éppen \(\displaystyle MP\cdot MQ\).
Vegyünk most egy tetszőleges, \(\displaystyle P\)-re és \(\displaystyle Q\)-ra illeszkedő \(\displaystyle k'\) kört, amely metszi \(\displaystyle k\)-t valamilyen \(\displaystyle A\) és \(\displaystyle B\) pontokban, s legyen \(\displaystyle N=PQ\cap AB\). Az előzőhöz hasonlóan \(\displaystyle NP\cdot NQ=NA\cdot NB\). Az \(\displaystyle N\) pont tehát illeszkedik a \(\displaystyle PQ\) egyenesre, és a \(\displaystyle k\) körre vonatkozó hatványa épp \(\displaystyle NP\cdot NQ\).
Ezekből a következő szerkesztési eljárás adódik.
A szerkesztés menete:
- Messe \(\displaystyle PQ\) szakaszfelező merőlegese \(\displaystyle k\)-t a \(\displaystyle C\) és \(\displaystyle C'\) pontokban. Szerkesszünk \(\displaystyle C\) körül \(\displaystyle CP\) sugarú \(\displaystyle k'\) kört, amely \(\displaystyle k\)-t az \(\displaystyle A\) és \(\displaystyle B\) pontokban metszi.
- Szerkesszük meg az \(\displaystyle AB\) és \(\displaystyle PQ\) egyenesek \(\displaystyle M\) metszéspontját.
- Szerkesszük meg a \(\displaystyle k\) kör \(\displaystyle O\) középpontját. (Ezt megtehetjük pl. két tetszőleges, nem párhuzamos húrja szakaszfelező merőlegeseinek metszeteként.)
- Szerkesszük meg az \(\displaystyle MO\) egyenes és a \(\displaystyle k\) kör \(\displaystyle X\) és \(\displaystyle Y\) metszéspontjait.
- Szerkesszük meg az \(\displaystyle XPQ\triangle\) körülírt körét. Ez adja a keresett kört.
A szerkesztés helyességének igazolása:
A bevezetőben leírtak szerint az \(\displaystyle M\) pont \(\displaystyle k'\)-re és \(\displaystyle k\)-ra vonatkozó hatványa megegyezik:
\(\displaystyle MP\cdot MQ=MA\cdot MB=MX\cdot MY.\)
Így a szelőtétel megfordítása miatt \(\displaystyle P\), \(\displaystyle Q\), \(\displaystyle X\) és \(\displaystyle Y\) egy \(\displaystyle \kappa\) körre illeszkednek, amely így valóban az átellenes \(\displaystyle X\) és \(\displaystyle Y\) pontokban metszi \(\displaystyle k\)-t.
Diszkusszió. Először megmutatjuk, hogy ha \(\displaystyle P\), \(\displaystyle Q\) és \(\displaystyle O\) kollineárisak, akkor nincs megoldása a feladatnak. Tegyük fel, hogy létezik a keresett \(\displaystyle \kappa\) kör, amely az \(\displaystyle X\) és \(\displaystyle Y\) átellenes pontokban metszi \(\displaystyle k\)-t. Ekkor \(\displaystyle XYPQ\) húrnégyszög, így konvex, tehát az \(\displaystyle XY\) szakasz \(\displaystyle O\) felezőpontja benne van a négyszögben, vagyis a \(\displaystyle PQ\) szakasz is szükségképpen tartalmazza \(\displaystyle O\)-t. Így \(\displaystyle XY\) a \(\displaystyle P\) és \(\displaystyle Q\) pontok egyikéből \(\displaystyle \varphi\), másikából \(\displaystyle 180^\circ - \varphi\) szög alatt látszik, vagyis legalább az egyik nincs az \(\displaystyle XY\) fölé írt Thalész-kör belsejében, ami ellentmond a kiinduló feltételeinknek.
Másodszor megmutatjuk, hogy a feladatnak legfeljebb egy megoldása van. Tegyük fel, hogy két különböző \(\displaystyle k_1\) és \(\displaystyle k_2\) megoldás van, ezek átellenes pontjai \(\displaystyle X_1\) és \(\displaystyle Y_1\), ill. \(\displaystyle X_2\) és \(\displaystyle Y_2\). Nyilván \(\displaystyle X_1Y_1\cap X_2Y_2=O\), és \(\displaystyle k_1\) és \(\displaystyle k_2\) \(\displaystyle P\)-ben és \(\displaystyle Q\)-ban metszik egymást.
Vegyük észre, hogy egyrészről az \(\displaystyle X_1Y_1\cap X_2Y_2=O\) észrevétel miatt az \(\displaystyle X_2\) és \(\displaystyle Y_2\) pontok közül pontosan az egyik van \(\displaystyle k_1\) belsejében.
Másrészről a \(\displaystyle PQ\) és \(\displaystyle X_2Y_2\) szakaszok nem metszhetik egymást, mert \(\displaystyle P\)-ből és \(\displaystyle Q\)-ból is tompaszög alatt látszik az \(\displaystyle X_2Y_2\) szakasz (\(\displaystyle P\) és \(\displaystyle Q\) benne van \(\displaystyle X_2Y_2\) Thalész-körében), így ezek a szögek nem lehetnek egy húrnégyszög szemköztes szögei. Tehát \(\displaystyle X_2\) és \(\displaystyle Y_2\) a \(\displaystyle k_2\) kör egyazon \(\displaystyle PQ\) ívén fekszik, s így \(\displaystyle X_2\) és \(\displaystyle Y_2\) közül vagy mindkettő \(\displaystyle k_1\) belsejében van, vagy egyik sem. Ez ellentmond az előző bekezdés következtetésének, ezért a kiinduló feltételezésünk hibás, legfeljebb egy megoldás lehet.
Rátérünk a szerkesztési eljárás vizsgálatára.
A szerkesztés során használt \(\displaystyle k'\) kör mindig létezik. Az \(\displaystyle M\) metszéspont nem jön létre, ha \(\displaystyle AB\parallel PQ\). Ez pontosan akkor térténik meg, ha az \(\displaystyle O\) középpont illeszkedik \(\displaystyle PQ\) szakaszfelező merőlegesére. Ekkor a szerkesztés menetét a következőképpen módosítjuk: A negyedik lépésben \(\displaystyle O\)-n keresztül szerkesszünk párhuzamost \(\displaystyle PQ\)-val, ez messe \(\displaystyle k\)-t az \(\displaystyle X\) és \(\displaystyle Y\) átellenes pontokban. A keresett kört ismét \(\displaystyle XPQ\triangle\) körülírt köre adja. Mivel az ábra szimmetrikus \(\displaystyle PQ\) szakaszfelező merőlegesére, így erre a körre \(\displaystyle Y\) illeszkedik, ami igazolja a szerkesztés helyességét.
Az \(\displaystyle XPQ\) háromszög körülírt köre nem létezik, ha a háromszög elfajuló, azaz \(\displaystyle X\), \(\displaystyle P\) és \(\displaystyle Q\) kollineárisak. Először vizsgáljuk azt az esetet, amikor az \(\displaystyle M\) pont létezik. Ilyenkor az \(\displaystyle O\), \(\displaystyle M\), \(\displaystyle Y\), \(\displaystyle X\), \(\displaystyle P\) és \(\displaystyle Q\) pontok mind illeszkednek egy egyenesre. Ha az \(\displaystyle M\) pont nem létezik, és \(\displaystyle XPQ\) elfajul, akkor szintén világos, hogy a szerkesztés során az \(\displaystyle O\), \(\displaystyle Y\), \(\displaystyle X\), \(\displaystyle P\) és \(\displaystyle Q\) pontok kollineárisak. Összességében tehát a szerkesztési eljárásunk pontosan akkor nem vezet eredményre, ha \(\displaystyle P\), \(\displaystyle Q\) és \(\displaystyle O\) kollineárisak.
Összegezve: a feladatnak nincs megoldása, ha \(\displaystyle P\), \(\displaystyle Q\) és \(\displaystyle O\) kollineárisak, minden más esetben pontosan egy megoldása van, amit a megadott eljárás szolgáltat.
Statisztika:
32 dolgozat érkezett. 5 pontot kapott: Bodor Mátyás, Chrobák Gergő, Czanik Pál, Diaconescu Tashi, Fülöp Csilla, Holló Martin, Melján Dávid Gergő, Szakács Ábel, Varga Boldizsár, Virág Rudolf, Wiener Anna, Zömbik Barnabás. 4 pontot kapott: Csonka Illés, Gömze Norken, László Anna, Nádor Artúr, Nguyen Kim Dorka, Sárdinecz Dóra, Tarján Bernát, Tran Dávid, Veres Dorottya. 3 pontot kapott: 2 versenyző. 2 pontot kapott: 4 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2023. januári matematika feladatai

