A B. 5297. feladat (2023. február)

B. 5297. Az \(\displaystyle ABC\) háromszögben \(\displaystyle BAC\sphericalangle=2CBA\sphericalangle\). Legyenek \(\displaystyle A'\), \(\displaystyle B'\), \(\displaystyle C'\) rendre az \(\displaystyle CA\), \(\displaystyle AB\) és \(\displaystyle BC\) oldalak olyan belső pontjai, amelyekre az \(\displaystyle A'B'C'\) háromszög hasonló az \(\displaystyle ABC\) háromszöghöz. Mutassuk meg, hogy a \(\displaystyle BAC\) és a \(\displaystyle B'A'C'\) szögek felezői a \(\displaystyle B'C'\) szakaszon metszik egymást.

Javasolta: Kós Géza (Budapest)

(4 pont)

A beküldési határidő 2023. március 10-én LEJÁRT.

Megoldás. Legyen \(\displaystyle M\) a \(\displaystyle B'C'\) szakasz és a \(\displaystyle B'A'C'\) szög felezőjének metszéspontja; azt kell igazolnunk, hogy \(\displaystyle AM\) felezi a \(\displaystyle BAC\) szöget.

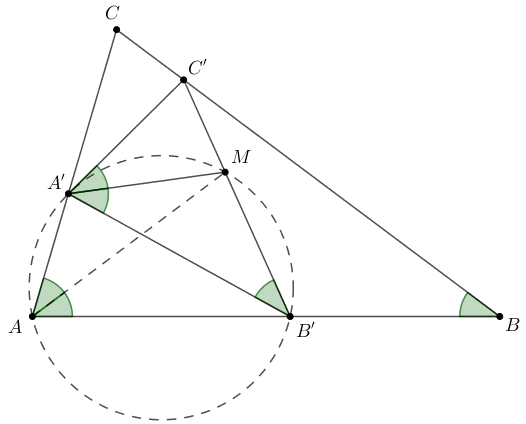
A feltétel szerint \(\displaystyle ABC\triangle\sim A'B'C'\triangle\) és \(\displaystyle BAC\sphericalangle=2CBA\sphericalangle\), ezért

\(\displaystyle MB'A'\sphericalangle =C'B'A'\sphericalangle =CBA\sphericalangle =\frac12BAC\sphericalangle =\frac12B'A'C'\sphericalangle =B'A'M\sphericalangle =MA'C'\sphericalangle. \)

Az \(\displaystyle A'B'M\) háromszög szögeit összeszámolva láthatjuk, hogy

\(\displaystyle 180^\circ-A'MB'\sphericalangle =B'A'M\sphericalangle+MB'A'\sphericalangle =\frac12BAC\sphericalangle+\frac12BAC\sphericalangle =BAC\sphericalangle =B'AA'\sphericalangle, \)

ezért \(\displaystyle AB'MA'\) húrnégyszög.

Végül, az \(\displaystyle AB'MA'\) húrnégyszögben

\(\displaystyle BAM\sphericalangle = B'AM\sphericalangle = B'A'M\sphericalangle = MB'A'\sphericalangle = MAA'\sphericalangle = MAC\sphericalangle, \)

vagyis \(\displaystyle AM\) valóban felezi a \(\displaystyle BAC\) szöget.

Statisztika:

70 dolgozat érkezett.
4 pontot kapott:	Ali Richárd, Aravin Peter, Balaskó Imola, Bodor Mátyás, Bui Thuy-Trang Nikolett, Chrobák Gergő, Csupor Albert Dezső, Diaconescu Tashi, Domján Olivér, Fodor Dóra, Hosszu Noel, Inokai Ádám, Kerekes András, Kocsis 827 Péter, Kosztolányi Karina, Kovács Benedek Noel, Melján Dávid Gergő, Nagy 292 Korina, Nagy 429 Leila, Nguyen Kim Dorka, Pálfi András, Pletikoszity Martin, Romaniuc Albert-Iulian, Sárdinecz Dóra, Sütő Áron, Szabó Zóra, Szittyai Anna, Tarján Bernát, Teveli Jakab, Tusnády Sámuel, Varga Boldizsár, Veres Dorottya, Vigh 279 Zalán, Virág Lénárd Dániel, Virág Rudolf, Zhai Yu Fan.
3 pontot kapott:	21 versenyző.
2 pontot kapott:	6 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	3 versenyző.

A KöMaL 2023. februári matematika feladatai