 |
A B. 5303. feladat (2023. március) |
B. 5303. Az \(\displaystyle ABC\) egyenlő szárú derékszögű háromszögnek \(\displaystyle C\)-nél van a derékszöge. Vegyünk fel a \(\displaystyle BC\) oldal belsejében egy \(\displaystyle D\) pontot úgy, hogy a \(\displaystyle CDA\) szög \(\displaystyle 75^\circ\) legyen. Tegyük fel, hogy az \(\displaystyle ADC\) háromszög területe egységnyi. Bizonyítsuk be, hogy \(\displaystyle BD = 2\).
Javasolta: Hujter Mihály (Budapest)
(4 pont)
A beküldési határidő 2023. április 11-én LEJÁRT.
Megoldás. A \(\displaystyle DAB\) szög felezője messe a \(\displaystyle BC\) oldalt \(\displaystyle E\)-ben, legyen továbbá \(\displaystyle AC=BC=m\).
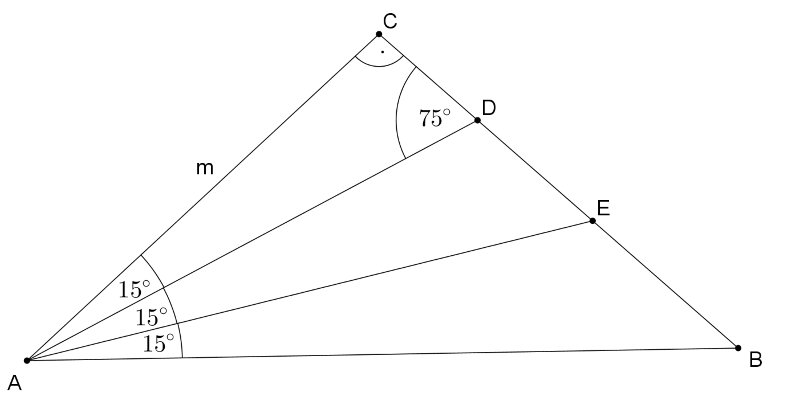
Nyilván \(\displaystyle CAD\sphericalangle = 15^{\circ}\), így \(\displaystyle DAE\sphericalangle = EAB\sphericalangle = 15^{\circ}\). A \(\displaystyle CAE\) derékszögű háromszög \(\displaystyle A\)-nál levő szöge \(\displaystyle 30^{\circ}\) lévén \(\displaystyle AE=m\cdot \dfrac{2}{\sqrt{3}}\) és \(\displaystyle CE=AE/2= \dfrac{m}{\sqrt{3}}\). Mivel \(\displaystyle AD\) felezi a \(\displaystyle CAE\) szöget, a szögfelező tétel szerint \(\displaystyle \dfrac{CD}{DE}=\dfrac{m}{m\cdot \dfrac{2}{\sqrt{3}}} = \dfrac{\sqrt{3}}{2}\). Így
\(\displaystyle DE = CE - CD = \dfrac{m}{\sqrt{3}} - CD,\)
\(\displaystyle \dfrac{\sqrt{3}}{2} = \dfrac{CD}{DE} = \dfrac{CD}{\dfrac{m}{\sqrt{3}} - CD},\)
amiből \(\displaystyle CD=\dfrac{m}{2+\sqrt{3}}\).
A megfelelő háromszögek területére
\(\displaystyle \dfrac{t_{ACD}}{t_{ABC}} = \dfrac{CD}{m} = \dfrac{1}{2+\sqrt{3}}, \)
\(\displaystyle 1=t_{ACD} = \dfrac{1}{2+\sqrt{3}} \cdot \dfrac{1}{2}\cdot m^2, \)
innen pedig \(\displaystyle m^2 = 4+2\sqrt{3}=(1+\sqrt{3})^2\), \(\displaystyle m=1+\sqrt{3}\). Végül
\(\displaystyle BD = m - CD = 1+\sqrt{3} - \dfrac{m}{2+\sqrt{3}} = 1+\sqrt{3} - \dfrac{1+\sqrt{3}}{2+\sqrt{3}} = (1+\sqrt{3})\cdot \big(1- \dfrac{1}{2+\sqrt{3}} \big) = (1+\sqrt{3})\cdot \dfrac{1+\sqrt{3}}{2+\sqrt{3}} = 2. \)
Statisztika:
130 dolgozat érkezett. 4 pontot kapott: 117 versenyző. 3 pontot kapott: 4 versenyző. 0 pontot kapott: 1 versenyző. Nem versenyszerű: 6 dolgozat.
A KöMaL 2023. márciusi matematika feladatai

