 |
A B. 5442. feladat (2025. február) |
B. 5442. Legyenek \(\displaystyle n\), \(\displaystyle k\) és \(\displaystyle \ell\) pozitív egész számok. Jelölje \(\displaystyle g(n,k,\ell)\) azt, hogy hányféleképpen lehet egy \(\displaystyle n \times k\) méretű táblázatot az \(\displaystyle \{1,2, \ldots, \ell+1\}\) halmaz elemeivel úgy kitölteni, hogy minden sorban és minden oszlopban balról jobbra, illetve fentről lefelé monoton nőjenek a számok. Bizonyítsuk be, hogy \(\displaystyle g(n,k,\ell)=g(k,\ell,n)\).
Javasolta: Gyenes Zoltán (Budapest)
(5 pont)
A beküldési határidő 2025. március 10-én LEJÁRT.
Megoldás. \(\displaystyle g(k,\ell,n)\) meghatározásakor egy \(\displaystyle k \times \ell\) méretű táblázatot töltünk ki az \(\displaystyle \{1,2, \ldots, n+1\}\) halmaz elemeivel. A lehetséges kitöltések száma nem változik meg, ha inkább a \(\displaystyle \{0,1,\ldots,n\}\) számokkal töltjük ki a táblázatot (a monotonitási feltételek megtartása mellett, természetesen). Az ilyen táblázatkitöltések halmazát jelöljük \(\displaystyle \mathcal{A}\)-val (tehát \(\displaystyle |\mathcal{A}| = g(k,\ell,n)\).)
Mivel sorok és oszlopok szerepe felcserélhető a feladatban (másképp mondva: világos, hogy \(\displaystyle g(n,k,\ell) = g(k,n,\ell)\)), a \(\displaystyle g(n,k,\ell)\) kiszámításakor is tekinthetjük úgy, hogy egy \(\displaystyle k \times n\)-es (azaz \(\displaystyle k\) sorból és \(\displaystyle n\) oszlopból álló) táblázatot töltünk ki a \(\displaystyle \{0,1,\ldots,\ell\}\) halmaz elemeivel. Az ilyen (monotonitási feltételeket is teljesítő) táblázat-kitöltések halmazát jelöljük \(\displaystyle \mathcal{B}\)-vel (tehát \(\displaystyle |\mathcal{B}| = g(k,n,\ell) = g(n,k,\ell)\).)
A bizonyítandó egyenlőséget úgy igazoljuk, hogy egy bijekciót állítunk fel az \(\displaystyle \mathcal{A}\) és \(\displaystyle \mathcal{B}\) halmazok között. Vegyünk egy tetszőleges \(\displaystyle A \in \mathcal{A}\) kitöltést, az \(\displaystyle i\)-edik sor \(\displaystyle j\)-edik elemét jelöljük \(\displaystyle a_{i,j}\)-vel. Alább egy példa látható \(\displaystyle k=3\), \(\displaystyle \ell=4\), \(\displaystyle n=6\) esetén, itt például \(\displaystyle a_{2,3} = 2\).
| 0 | 1 | 1 | 3 |
| 0 | 1 | 2 | 5 |
| 1 | 3 | 4 | 6 |
Az \(\displaystyle A\)-hoz a következő módon rendelünk egy \(\displaystyle \mathcal{B}\)-beli \(\displaystyle B\) kitöltést: az \(\displaystyle i\)-edik sor \(\displaystyle j\)-edik helyére írt szám (továbbiakban: \(\displaystyle b_{i,j}\)) legyen az, hogy \(\displaystyle A\)-ban az \(\displaystyle i\)-edik sorban, azaz az
\(\displaystyle a_{i,1} \leq a_{i,2} \leq \ldots \leq a_{i,\ell} \)
sorozatban hány \(\displaystyle (n-j)\)-nél nagyobb szám szerepel. Így például a fenti \(\displaystyle A\) táblázatnak a következő \(\displaystyle B\) felel meg:
| 0 | 0 | 0 | 1 | 1 | 3 |
| 0 | 1 | 1 | 1 | 2 | 3 |
| 1 | 1 | 2 | 3 | 3 | 4 |
Ellenőrizzük, hogy tényleg \(\displaystyle \mathcal{B}\)-beli táblázatkitöltést kaptunk így.
- Minden mezőbe \(\displaystyle 0\) és \(\displaystyle \ell\) közötti számot írtunk (hiszen \(\displaystyle A\) egy sorának \(\displaystyle \ell\) darab eleme van).
- \(\displaystyle b_{i,j} \leq b_{i,j+1}\) mindig teljesül, hiszen ugyanazon sorban számoltuk meg az \(\displaystyle (n-j)\)-nél, ill. az \(\displaystyle (n-j-1)\)-nél nagyobb számokat.
- \(\displaystyle b_{i,j} \leq b_{i+1,j}\) is teljesül mindig, hiszen ha \(\displaystyle a_{i,h} \leq h-j\) valamilyen \(\displaystyle h\)-ra, akkor \(\displaystyle a_{i+1,h} \leq h-j\) is teljesül az oszlopokra vonatkozó monotonitási feltétel miatt.
Ezzel tehát valóban egy \(\displaystyle \mathcal{A} \to \mathcal{B}\) hozzárendelést adtunk meg. Az van hátra, hogy belássuk, hogy ez bijekció. Ehhez tetszőleges \(\displaystyle B \in \mathcal{B}\) esetén egyértelműen meg kell tudnunk mondani, hogy melyik \(\displaystyle A \in \mathcal{B}\)-hoz rendeljük; avagy a \(\displaystyle b_{i,j}\) számok ismeretének meg kell tudnunk mondani az \(\displaystyle a_{i,j}\)-ket.
Ez menni fog! Vegyük ugyanis észre, hogy az a módszer, amellyel \(\displaystyle A\)-hoz hozzárendeljük \(\displaystyle B\)-t, a \(\displaystyle B\)-hez éppen az \(\displaystyle A\)-t rendeli hozzá. (Azaz a hozzárendelésünk lényegében önmaga inverze – azért csak lényegében, mert \(\displaystyle \ell \neq n\) esetén persze eltér a két irányú függvény értelmezési tartománya és értékkészlete, csak a függvényt meghatározó eljárás ugyanaz.) Azt kell tehát végiggondolnunk, hogy minden \(\displaystyle i,j\) esetán \(\displaystyle a_{i,j}\) megyegyezik azzal az \(\displaystyle c = c_{i,j}\) számmal, amely a
\(\displaystyle b_{i,1} \leq b_{i,2} \leq \ldots \leq b_{i,n} \)
számok között az \(\displaystyle (\ell - j)\)-nél nagyobbak darabszáma.
Világos, hogy ekkor \(\displaystyle b_{i,n-c} \leq \ell - j < b_{i,n-c+1}\), azaz az
\(\displaystyle a_{i,1} \leq a_{i,2} \leq \ldots \leq a_{i,\ell-j} \leq \ldots \leq a_{i,\ell} \)
számok közt az \(\displaystyle n-(n-c) = c\)-nél nagyobbak száma legfeljebb \(\displaystyle \ell - j\), de az \(\displaystyle n-(n-c+1) = (c-1)\)-nél nagyobbak száma már több, mint \(\displaystyle \ell - j\). Ez meg csak akkor lehet, ha az \(\displaystyle (\ell - j + 1)\)-edik legnagyobb elem, azaz elölről számolva \(\displaystyle j\)-edik elem, \(\displaystyle a_{i,j}\) értéke pontosan \(\displaystyle c\). Éppen ezt akartuk bizonyítani.
Megjegyzés. Adott \(\displaystyle (k,\ell,n)\), pozitív egészekből álló számhármasra tekintsük azt a (középpontosan szimmetrikus) hatszöget, amelynek mindegyik belső szöge \(\displaystyle 120^\circ\), míg az oldalai valamilyen körüljárás szerint \(\displaystyle k\), \(\displaystyle \ell\), \(\displaystyle n\), \(\displaystyle k\), \(\displaystyle \ell\), \(\displaystyle n\) egység hosszúak (ilyen hatszöget szabályos háromszögrácsra könnyű rajzolni).

Jelölje \(\displaystyle f(k,\ell,n)\), hogy hányféleképpen lehet ezt a hatszöget lefedni olyan rombuszokkal, amelyek minden oldala egységnyi, míg belső szögeik \(\displaystyle 60^\circ\) és \(\displaystyle 120^\circ\).
Állítás. \(\displaystyle f(k,\ell,n) = g(k,\ell,n)\) teljesül tetszőleges \(\displaystyle k,\ell,n\) pozitív egész számok esetén.
Bizonyításvázlat. Vegyünk egy olyan ládát, amelynek alapja egy \(\displaystyle k \times n\)-es téglalap, és magassága \(\displaystyle \ell\).
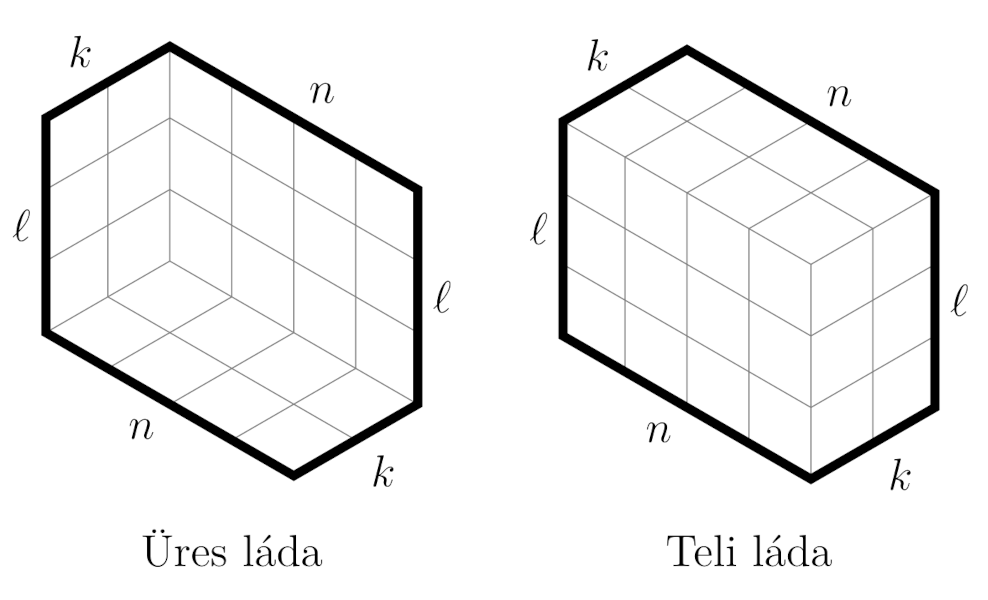
Ebbe a ládába pakoljunk (a rácsvonalakhoz illeszkedően) néhány \(\displaystyle 1 \times 1 \times 1\)-es kockát úgy, hogy minden kocka alatt és minden kocka mögött is legyen másik kocka. Egy ilyen kockapakolás alkalmas irányú axonometrikus nézete éppen egy rombuszokra való felosztását adja a hatszögünknek.
De egy kockapakolás megfeleltethető egy monoton csökkenő táblázatkitöltésnek is: a \(\displaystyle \{0,1,\ldots,\ell\}\) halmazból választott szám azt írja le, hogy hány kocka van az alap egy mezője felett.
Hogy ezzel tényleg bijekciót hoztunk létre a táblázatkitöltések és a rombusz-felosztások között, az szemléletesen akár triviálisnak is tűnhet – precíz bizonyítása azonban igen macerás, különösen ez a rész: miért is lehet minden rombuszfelosztást egy kockapakolásnak megfeleltetni? Ebben a témakörben nem ritka, hogy szemléletesen egyszerűnek tűnő állítások precízen végiggondolva igen bonyolulttá válnak, ld. pl. a 2021. februári B.5156. feladat megoldását.
Mivel \(\displaystyle f(k,\ell,n)\) nem érzékeny a változók sorrendjére, ezért ebből rögtön következik a feladat állítása.
Valójában a feladat úgy született, hogy a kitűző (gyerekei rombusz puzzle játéka kapcsán) a szabályos hatszög rombuszokkal való lefedésein gondolkodott.
Statisztika:
39 dolgozat érkezett. 5 pontot kapott: Ali Richárd, Aravin Peter, Balla Ignác , Bodor Noémi, Bolla Donát Andor, Bui Thuy-Trang Nikolett, Fodor Barna, Görömbey Tamás, Hajba Milán, Hodossy Réka, Holló Martin, Kovács Benedek Noel, Kővágó Edit Gréta, Li Mingdao, Molnár István Ádám, Pázmándi József Áron, Péter Hanna, Prohászka Bulcsú, Rajtik Sándor Barnabás, Sánta Gergely Péter, Sárdinecz Dóra, Sha Jingyuan, Sun Wen Ze, Sütő Áron, Szabó 721 Sámuel, Szaszkó Benedek, Tamás Gellért, Vámosi Bendegúz Péter, Varga 511 Vivien, Vigh 279 Zalán, Vödrös Dániel László, Wágner Márton, Zhai Yu Fan. 4 pontot kapott: Gyenes Károly. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2025. februári matematika feladatai
