 |
A B. 5465. feladat (2025. május) |
B. 5465. Legyenek \(\displaystyle AA'\), \(\displaystyle BB'\), \(\displaystyle CC'\) átmérők az \(\displaystyle ABC\) hegyesszögű, nem szabályos háromszög köré írt körben. Legyen az \(\displaystyle A'\) pontnak a \(\displaystyle BC\) egyenesre vett tükörképe \(\displaystyle A_1\), a \(\displaystyle B'\)-nek az \(\displaystyle AC\)-re vett tükörképe \(\displaystyle B_1\), a \(\displaystyle C'\)-nek az \(\displaystyle AB\)-re vett tükörképe pedig \(\displaystyle C_1\). Mutassuk meg, hogy az \(\displaystyle A_1B_1C_1\) háromszög hasonló az \(\displaystyle ABC\) háromszöghöz.
Javasolta: Kocsis Szilveszter (Budapest)
(5 pont)
A beküldési határidő 2025. június 10-én LEJÁRT.
Megoldás. A megoldást több, önmagában is tanulságos - de épp ezért jól ismert - állításra tagoljuk.
1. Állítás. Tetszőleges \(\displaystyle ABC\) háromszögben az \(\displaystyle M\) magasságpont tükörképe a \(\displaystyle BC\) oldal felezőpontjára az \(\displaystyle ABC\) kör \(\displaystyle A\)-val átellenes \(\displaystyle A'\) pontja.

Bizonyítás. A leggyorsabb bizonyítás vektorokkal történhet. Az \(\displaystyle ABC\) kör \(\displaystyle O\) középpontjából mutasson az \(\displaystyle A\), \(\displaystyle B\) és \(\displaystyle C\) csúcsokba rendre az \(\displaystyle \mathbf a\), \(\displaystyle \mathbf b\) és \(\displaystyle \mathbf c\) vektor. Jól ismert, hogy az \(\displaystyle M\) magasságpontba éppen az \(\displaystyle \mathbf m= \mathbf a+ \mathbf b+ \mathbf c\) vektor mutat; továbbá nyilvánvaló, hogy a kör \(\displaystyle A\)-val átellenes \(\displaystyle A'\) pontjába az \(\displaystyle \mathbf a'=-\mathbf a\) vektor. Ezért az \(\displaystyle MA'\) szakasz \(\displaystyle F\) felezőpontjába az \(\displaystyle \mathbf f = (\mathbf m+ \mathbf a')/2=(\mathbf b + \mathbf c)/2\) vektor mutat, vagyis \(\displaystyle F\) a \(\displaystyle BC\) szakaszt is felezi. Ebből az állítás következik. \(\displaystyle \square\)
2. Állítás. A feladatban szereplő \(\displaystyle A_1\) pont éppen az \(\displaystyle ABC\) háromszög \(\displaystyle M\) magasságpontjának tükörképe a \(\displaystyle BC\) oldal felezőmerőlegesére.
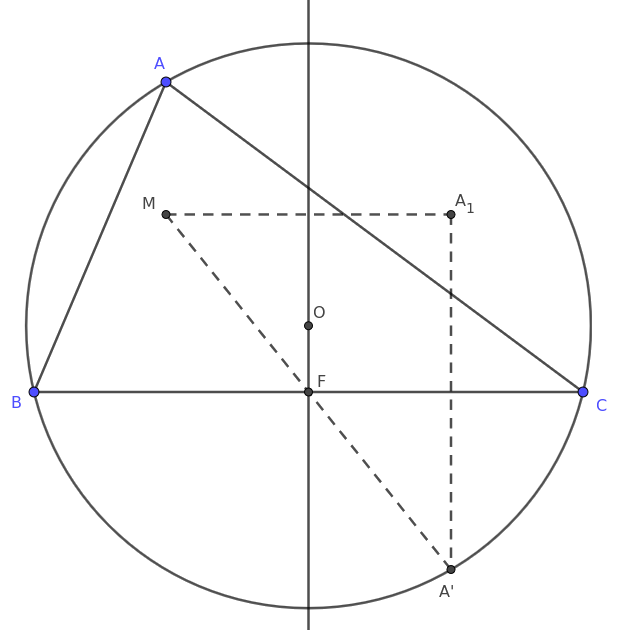
Bizonyítás. Jelölje \(\displaystyle \tau_F\) az \(\displaystyle F\) pontra vonatkozó középpontos tükrözést, továbbá \(\displaystyle \tau_a\) és \(\displaystyle \tau_f\) a \(\displaystyle BC\) oldalra, ill. annak felezőmerőlegesére vonatkozó tengelyes tükrözéseket. Ekkor persze \(\displaystyle \tau_F = \tau_f\circ \tau_a\). Továbbá az 1. Állítás szerint \(\displaystyle \tau_F(A')=M\), amiből \(\displaystyle \tau_f(M)=\tau_f(\tau_F(A'))=\tau_f(\tau_f(\tau_a(A')))=\tau_a(A')=A_1\), ami igazolja az állítást. \(\displaystyle \square\)
Nyilvánvalóan a \(\displaystyle B_1\)-re és \(\displaystyle C_1\)-re hasonló állítás teljesül, vagyis az \(\displaystyle A_1B_1C_1\) háromszöget úgy kaphatjuk, ha \(\displaystyle M\)-t tükrözzük \(\displaystyle ABC\) oldalfelező merőlegeseire.
3. Állítás. Legyen \(\displaystyle P\) tetszőleges (az \(\displaystyle ABC\) kör \(\displaystyle O\) középpontjától különböző) pont, és tükrözzük az \(\displaystyle ABC\) háromszög oldalfelező merőlegeseire, így kapjuk a \(\displaystyle P_aP_bP_c\) háromszöget. Ekkor a \(\displaystyle P_aP_bP_c\) háromszög hasonló az \(\displaystyle ABC\) háromszöghöz.
Bizonyítás. A diszkussziót elkerülendő irányított szögekkel számolunk. Az egyszerűbb érthetőség kedvéért először tegyük fel, hogy \(\displaystyle P\) rajta van az \(\displaystyle ABC\) körön. A \(\displaystyle P\)-t rendre \(\displaystyle A\)-ba, \(\displaystyle B\)-be és \(\displaystyle C\)-be vivő \(\displaystyle O\) körüli forgatás szöge legyen \(\displaystyle \alpha\), \(\displaystyle \beta\) és \(\displaystyle \gamma\). Ekkor (az egyik) \(\displaystyle AB\) ív felezőpontjába \(\displaystyle P\)-t \(\displaystyle (\alpha+\beta)/2\) szögű forgatás viszi, és ezért \(\displaystyle P_c\)-be \(\displaystyle \alpha+\beta\) szögű. Ugyanígy, \(\displaystyle P\)-t \(\displaystyle P_a\)-ba \(\displaystyle \beta+\gamma\) szögű, míg \(\displaystyle P_b\)-be \(\displaystyle \alpha+\gamma\) szögű forgatás viszi. Ebből következően \(\displaystyle P_a\)-t \(\displaystyle P_b\)-be \(\displaystyle \alpha-\beta\); \(\displaystyle P_b\)-t \(\displaystyle P_c\)-be \(\displaystyle \beta-\gamma\); végül \(\displaystyle P_c\)-t \(\displaystyle P_a\)-ba \(\displaystyle \gamma-\alpha\) szögű forgatás viszi. Ebből következik, hogy a \(\displaystyle P_aP_bP_c\) háromszög egybevágó \(\displaystyle ABC\)-vel (és ellentétes körüljárású).
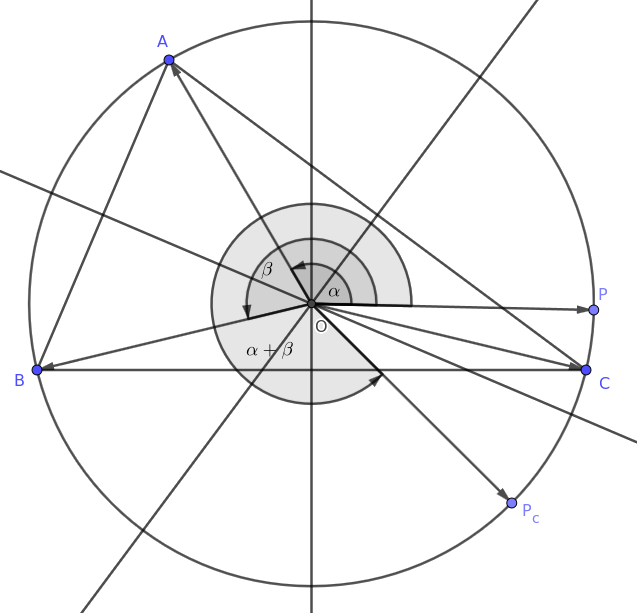
Ha \(\displaystyle P\) nem illeszkedik a körülírt körre, akkor nagyítsuk ki (vagy kicsinyítsük le) \(\displaystyle O\)-ból \(\displaystyle P\)-t abba a \(\displaystyle P'\)-be, amely illeszkedik az \(\displaystyle ABC\) körre. Az előzőek szerint a \(\displaystyle P'\)-höz tartozó \(\displaystyle P'_aP'_bP'_c\) háromszög egybevágó \(\displaystyle ABC\)-vel. Továbbá az is világos, hogy \(\displaystyle P_aP_bP_c\)-t az előbb \(\displaystyle P\)-re alkalmazott középpontos hasonlóság éppen \(\displaystyle P'_aP'_bP'_c\)-be viszi, így \(\displaystyle P_aP_bP_c\) valóban hasonló \(\displaystyle ABC\)-hez. \(\displaystyle \square\)
Mivel az \(\displaystyle A_1B_1C_1\) háromszöget úgy kapjuk, hogy a magasságpontot tükrözzük az \(\displaystyle ABC\) háromszög oldalfelező merőlegeseire, így a 3. Állítás szerint hasonló \(\displaystyle ABC\)-hez. Ezzel az állítást beláttuk.

Diszkusszió: A 3. Állítás nem igaz (elfajul), ha a \(\displaystyle P\) pont éppen az \(\displaystyle ABC\) kör \(\displaystyle O\) középpontja. Tehát nem alkalmazhatjuk, ha az \(\displaystyle ABC\) háromszög \(\displaystyle M\) magasságpontja egybeesik \(\displaystyle O\)-val. Jól ismert azonban, hogy ez csak a szabályos háromszögben történik meg, amit a feladat feltételeiben kizártunk, így a bizonyításunk teljes.
Statisztika:
25 dolgozat érkezett. 5 pontot kapott: Ali Richárd, Aravin Peter, Bodor Ádám, Bogdán Balázs Ákos, Holló Martin, Li Mingdao, Rajtik Sándor Barnabás, Sajter Klaus, Sánta Gergely Péter, Sha Jingyuan, Wágner Márton, Wiener Marcell. 4 pontot kapott: Bui Thuy-Trang Nikolett, Gyenes Károly, Kerekes András, Sárdinecz Dóra, Szabó 721 Sámuel, Vigh 279 Zalán, Zhai Yu Fan. 3 pontot kapott: 2 versenyző. 2 pontot kapott: 2 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2025. májusi matematika feladatai
