A B. 5468. feladat (2025. május)

B. 5468. Legyen az $\displaystyle ABC$ hegyesszögű háromszög beírt körének sugara $\displaystyle r$, körülírt körének sugara $\displaystyle R$ és a talpponti háromszögébe írt kör sugara $\displaystyle \varrho$. Mutassuk meg, hogy $\displaystyle r\ge \sqrt{R\varrho}$.

Javasolta: Vígh Viktor (Sándorfalva)

(6 pont)

A beküldési határidő 2025. június 10-én LEJÁRT.

1. megoldás. Jelöljük az $\displaystyle ABC$ háromszög beírt körének középpontját $\displaystyle I$-vel, magasságpontját $\displaystyle M$-mel, és körülírt körének középpontját $\displaystyle O$-val, végül a Feuerbach-körének középpontját $\displaystyle F$-fel.

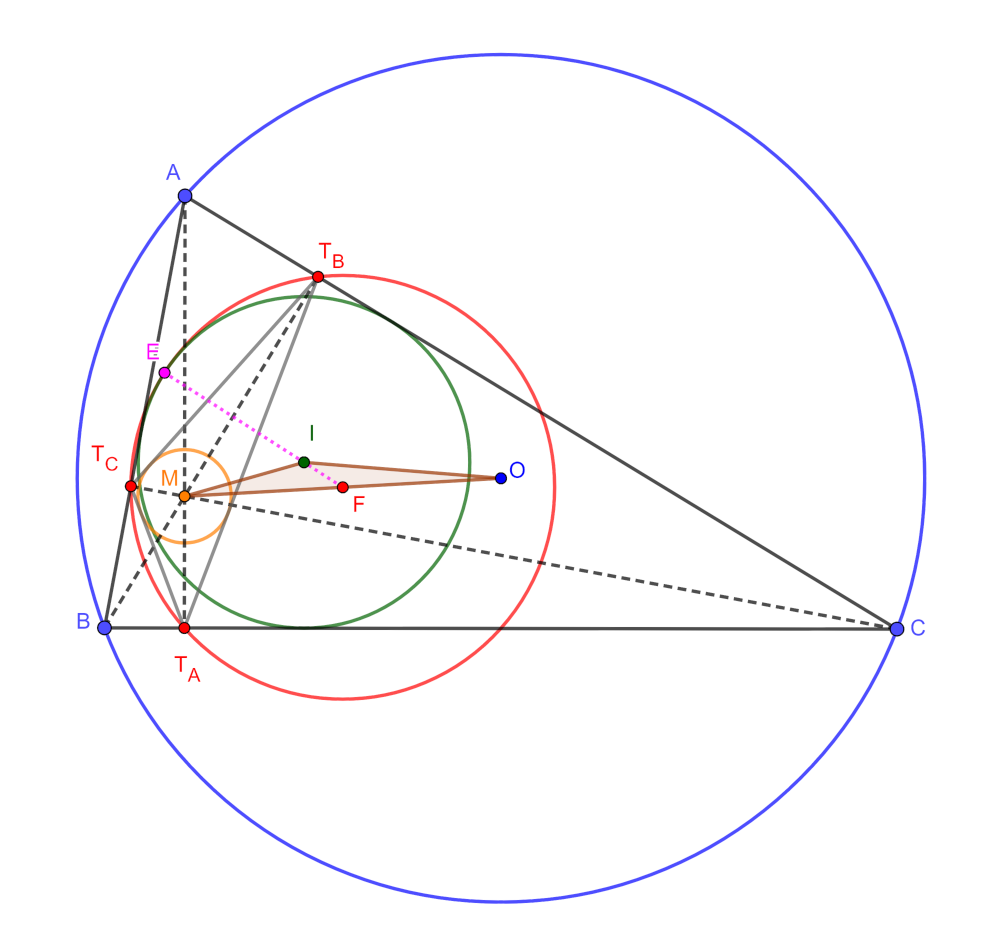
Ismert, hogy $\displaystyle IM$ felezőpontja $\displaystyle F$, és használni fogjuk a talpponti háromszög néhány jól ismert tulajdonságát is:

A talpponti háromszög köréírt köre éppen a Feuerbach-kör, melynek sugara a köréírt kör sugarának fele, azaz a feladat jelöléseivel $\displaystyle \frac{R}{2}$.
A talpponti háromszögben a magasságvonalak belső szögfelezők, tehát a talpponti háromszög beírt körének középpontja éppen $\displaystyle M$.

Tekintsük az $\displaystyle IMO$ háromszöget az $\displaystyle IF$ súlyvonalával. Írjuk fel ebben a háromszögben néhány szakasz hosszát.

Az Euler-tétel szerint $\displaystyle IO^2 = R^2-2Rr$.
Az Euler-tételt a talpponti háromszögre alkalmazva $\displaystyle MF^2 = \left(\frac{R}{2} \right)^2 - 2 \frac{R}{2} \varrho = \frac{R^2}{4} - R\varrho$, amiből $\displaystyle MO^2 = (2MF^2) = R^2 - 4 R \varrho.$
A Feuerbach-tétel szerint a beírt kör belülről érinti a Feuerbach-kört. Az $\displaystyle E$ érintési pont a két kör $\displaystyle IF$ centrálisán kell legyen, ezért $\displaystyle IF = FE - IE = \frac{R}{2}-r$.

Írjuk fel az alábbi (a paralelogramma-tételből vagy Stewart-tételből következő) összefüggést az $\displaystyle IMO$ háromszög $\displaystyle IF$ súlyvonalára:

$\displaystyle 2IM^2+2IO^2 = MO^2 + 4IF^2. $

Ebből

$$\begin{eqnarray*} 2 IM^2 &=& MO^2 + 4IF^2 - 2IO^2 = (R^2 - 4 R \varrho) + 4 \left( \frac{R}{2}-r \right)^2 - 2(R^2-2Rr) = \\ &=& R^2 - 4R\varrho + R^2 - 4Rr + 4r^2 - 2R^2 + 4Rr = 4r^2 - 4R\varrho. \end{eqnarray*}$$

Tehát $\displaystyle r^2 - R\varrho = \frac{IM^2}{2} \geq 0$, amivel beláttuk a bizonyítandó állítást. Egyenlőség akkor és csak akkor áll fenn, ha $\displaystyle I = M$, azaz a háromszög szabályos.

Megjegyzés: Az itt ismertetett megoldás kiolvasható a 2024. októberi B.5413. feladat online is publikált megoldásából.

2. megoldás. Az $\displaystyle r$ és az $\displaystyle \varrho$ értékét kifejezzük $\displaystyle R$-el és a háromszög szögeivel, és a feladat állítását egy trigonometrikus egyenlőtlenséggé fogalmazzuk át.

Használjuk az ábrán látható betűzést. Az $\displaystyle IBC$ háromszögben

$\displaystyle a = BY+YC = 2R\sin\alpha = 4R\sin\frac\alpha2\cos\frac\alpha2 $

és

$\displaystyle a = BX+XC = r\ctg\frac\beta2+r\ctg\frac\gamma2 = r \frac{\cos\frac\beta2\sin\frac\gamma2+\sin\frac\beta2\cos\frac\gamma2}{\sin\frac\beta2\sin\frac\gamma2} = r\frac{\sin\frac{\beta+\gamma}2}{\sin\frac\beta2\sin\frac\gamma2} = r\frac{\cos\frac{\alpha}2}{\sin\frac\beta2\sin\frac\gamma2}. $

Az $\displaystyle a$ oldal kétféle felírásából azt kapjuk, hogy

$\displaystyle r = 4R\sin\frac\alpha2\sin\frac\beta2\sin\frac\gamma2. $

A talpponti háromszög köré írt kör a Feuerbach-kör, sugara $\displaystyle R/2$. Például az $\displaystyle ABT_B$, $\displaystyle AT_AC$ derékszögű háromszögekből és a $\displaystyle BT_AMT_C$, $\displaystyle CT_BMT_A$ körökből leolvashatjuk, hogy a talpponti háromszög szögei $\displaystyle 180^\circ-2\alpha$, $\displaystyle 180^\circ-2\beta$ és $\displaystyle 180^\circ-2\gamma$, ezért a fenti okoskodást a talpponti háromszögre megismételve azt kapjuk, hogy

$\displaystyle \varrho = 4\frac{R}2\sin(90^\circ-\alpha)\sin(90^\circ-\beta)\sin(90^\circ-\gamma)= 2R\cos\alpha\cos\beta\cos\gamma. $

Ezek után a bizonyítandó állítás azzal ekvivalens, hogy

$\displaystyle 2\sqrt2 \sin\frac\alpha2\sin\frac\beta2\sin\frac\gamma2 \ge \sqrt{ \cos\alpha\cos\beta\cos\gamma}. $

Négyzetre emelve és a $\displaystyle 2\sin^2x=1-\cos 2x$ azonosságot alkalmazva,

$\displaystyle (1-\cos\alpha)(1-\cos\beta)(1-\cos\gamma) \ge\cos\alpha\cos\beta\cos\gamma, $

avagy

$\displaystyle \bigg(\frac{1}{\cos\alpha}-1\bigg) \bigg(\frac{1}{\cos\beta}-1\bigg) \bigg(\frac{1}{\cos\gamma}-1\bigg) \ge 1. $

Tehát, a feladat megoldásához elég ezt az egyenlőtlenséget igazolnunk.

Legyen $\displaystyle x=b^2+c^2-a^2$, $\displaystyle y=c^2+a^2-b^2$ és $\displaystyle z=a^2+b^2-c^2$. Mivel a háromszög hegyesszögű $\displaystyle x,y,z>0$. A koszinusztételből

$\displaystyle \frac{1}{\cos\alpha} = \frac{2bc}{b^2+c^2-a^2} = \frac{\sqrt{2c^2\cdot 2b^2}}{x} = \frac{\sqrt{(x+y)(x+z)}}{x}. $

A Cauchy–Schwarz egyenlőtlenséget alkalmazva a $\displaystyle \big(\sqrt{x},\sqrt{y}\big)$ és $\displaystyle \big(\sqrt{x},\sqrt{z}\big)$ párokra,

$\displaystyle \sqrt{(x+y)(x+z)} \ge x+\sqrt{yz}, $

és egyenlőség akkor áll, ha $\displaystyle \sqrt{x}:\sqrt{y}=\sqrt{x}:\sqrt{z}$, vagyis $\displaystyle y=z$. Így

$\displaystyle \frac1{\cos\alpha}-1 \ge \frac{x+\sqrt{yz}}{x}-1 = \frac{\sqrt{yz}}{x}. $

Ha ezt a másik két szögre is felírjuk, azt kapjuk, hogy

$\displaystyle \bigg(\frac{1}{\cos\alpha}-1\bigg) \bigg(\frac{1}{\cos\beta}-1\bigg) \bigg(\frac{1}{\cos\gamma}-1\bigg)\ \ge \frac{\sqrt{yz}}{x}\cdot\frac{\sqrt{zx}}{y}\cdot\frac{\sqrt{xy}}{z} = 1, $

és egyenlőség csak $\displaystyle x=y=z$, vagyis $\displaystyle a=b=c$ esetén áll fenn.

Statisztika:

A B. 5468. feladat értékelése még nem fejeződött be.

A KöMaL 2025. májusi matematika feladatai

Már regisztráltál?
Új vendég vagy?