A B. 5480. feladat (2025. október)

B. 5480. Az \(\displaystyle ABC\) háromszögben \(\displaystyle ACB \sphericalangle = 90^{\circ}\). Jelölje az \(\displaystyle AC\) befogó felezőpontját \(\displaystyle F\), az \(\displaystyle AB\) átfogó felezőpontját pedig \(\displaystyle G\). Igazoljuk, hogy \(\displaystyle FG\) Thalész-köre akkor és csak akkor érinti az \(\displaystyle ABC\) háromszögbe írt kört, ha \(\displaystyle AC=2BC\).

Javasolta: Sztranyák Attila (Budapest)

(4 pont)

A beküldési határidő 2025. november 10-én LEJÁRT.

Megoldás. Jelöljük az \(\displaystyle ABC\) háromszög oldalainak hosszát szokásosan \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\)-vel, beírt körének középpontját \(\displaystyle I\)-vel, érintési pontját az \(\displaystyle AC\) oldalon \(\displaystyle E\)-vel. Ismert, hogy derékszögű háromszög beírt körének sugara \(\displaystyle r=\frac{a+b-c}{2}\). Ez biztosan kisebb, mint bármelyik befogó fele, mivel az átfogó a leghosszabb oldal. Emiatt az \(\displaystyle E\) és \(\displaystyle F\) pontok biztosan különbözők, a feladatban szereplő két kör az \(\displaystyle AC\) oldalt különböző pontokban érinti, csak külső érintésről lehet szó.

Tegyük fel először, hogy a két kör kívülről érinti egymást. Használjuk a következő ábra jelöléseit.

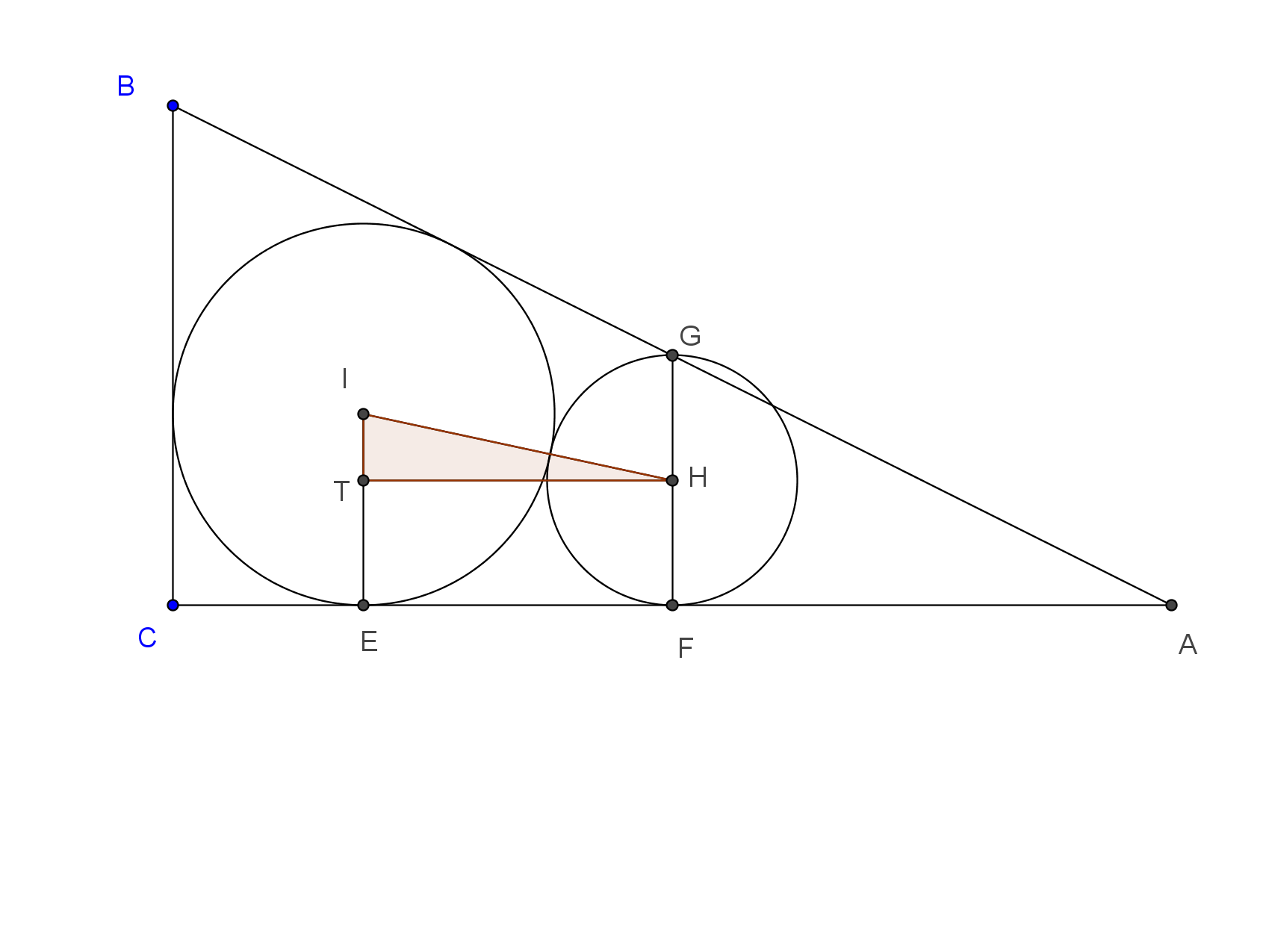
Legyen \(\displaystyle T\) a Thalész-kör \(\displaystyle H\) középpontjából a beírt kör \(\displaystyle IE\) sugarára állított merőleges talppontja. Az \(\displaystyle ITH\) háromszög oldalai: \(\displaystyle HT=CF-CE=\frac{b}{2}-r\), \(\displaystyle IT=\left|r-\frac{a}{4}\right|\), továbbá a külső érintés alapján \(\displaystyle IH=r+\frac{a}{4}\). Az \(\displaystyle ITH\) derékszögű háromszögre felírva Pitagorasz-tételt:

\(\displaystyle \left(\frac{b}{2}-r\right)^2+\left(r-\frac{a}{4}\right)^2=\left(r+\frac{a}{4}\right)^2.\)

A műveletek elvégzése után rendezve:

\(\displaystyle r(a+b-r)=\frac{b^2}{4}.\)

De derékszögű háromszögben \(\displaystyle a+b-r=a+b-\frac{a+b-c}{2}=\frac{a+b+c}{2}=s\). A terület kifejezései alapján így:

\(\displaystyle r(a+b-r)=rs=T=\frac{ab}{2}=\frac{b^2}{4},\)

tehát \(\displaystyle a=\frac{b}{2}\), vagyis \(\displaystyle AC=2BC\).

A megfordítás bizonyításához tegyük fel, hogy a derékszögű háromszögben \(\displaystyle AC=2BC\) és igazoljuk, hogy a két kör valóban kívülről érinti egymást. Az általánosság megszorítása nélkül feltehetjük, hogy \(\displaystyle BC=a=1\) és ezzel együtt \(\displaystyle AC=b=2\), \(\displaystyle AB=c=\sqrt{5}\), végül \(\displaystyle r=\frac{3-\sqrt{5}}{2}\). Tekintsük ismét az \(\displaystyle ITH\) derékszögű háromszöget. A befogók ismeretében felírjuk a Pitagorasz-tételt és ellenőrizzük, hogy az átfogó valóban a két kör sugarának összege lesz-e:

\(\displaystyle HT=\frac{b}{2}-r=1-\frac{3-\sqrt{5}}{2}=\frac{\sqrt{5}-1}{2},\quad IT=\left|r-\frac{a}{4}\right|=\frac{3-\sqrt{5}}{2}-\frac{1}{4}=\frac{5-2\sqrt{5}}{4}.\)

Számítsuk ki az \(\displaystyle ITH\) háromszög átfogójának négyzetét:

\(\displaystyle \left(\frac{\sqrt{5}-1}{2}\right)^2+\left(\frac{5-2\sqrt{5}}{4}\right)^2=\frac{6-2\sqrt{5}}{4}+\frac{45-20\sqrt{5}}{16}=\frac{49-2\cdot 7\cdot 2\sqrt{5}+20}{16}=\)

\(\displaystyle =\left(\frac{7-2\sqrt{5}}{4} \right)^2=\left(\frac{6-2\sqrt{5}}{4}+\frac{1}{4}\right)^2=\left(\frac{3-\sqrt{5}}{2}+\frac{1}{4}\right)^2=\left(r+\frac{a}{4}\right)^2. \)

A két kör valóban kívülről érinti egymást.

Megjegyzés. Ugyanezen feltétel esetén \(\displaystyle FG\) Thalész-köre az átfogó hozzáírt körét is érinti.

Statisztika:

72 dolgozat érkezett.
4 pontot kapott:	Ali Richárd, Bao Nguyen Gia, Bodor Ádám, Danka Emma, Diaconescu Tashi, Ercse Ferenc, Ethan Y.Wang, Hideg János, Holló Martin, Kerekes András, Kővágó Edit Gréta, Li Mingdao, Lovas Márk, Maróti Olga, Mikó Hédi Irma, Miszori Gergő, Molnár-Sáska Tamás, Nagy 707 Botond, Nagypál Katóca, Papp Mátyás, Péter Hanna, Rajtik Sándor Barnabás, Sajter Klaus, Tóth László Pál, Vincze Marcell, Wiener Marcell.
3 pontot kapott:	Balla Ignác , Beinschroth Máté, Budai Máté, Fodor Barna, Illés Dóra, József Áron, Körmöndi Márk, Lupkovics Lázár, Máté Kristóf, Miszori Márton, Molnár Lili, Papirnyy Oleksandr, Pázmándi József Áron, Sógor-Jász Soma, Takács András, Varga 511 Vivien.
2 pontot kapott:	21 versenyző.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	5 versenyző.

A KöMaL 2025. októberi matematika feladatai