A B. 5483. feladat (2025. október)

B. 5483. Egy pakliban \(\displaystyle 2n\) darab kártya van \(\displaystyle n\) különböző színnel, mindegyik színből egy \(\displaystyle 1\)-es és egy \(\displaystyle 2\)-es. \(\displaystyle n\) játékos a következő kooperatív játékot játssza. Először összekeverik a \(\displaystyle 2n\) lapot, majd mindenki húz két lapot, amelyeket megmutatnak egymásnak. Ezután közösen eldöntik, hogy milyen sorrendben ülnek le körben, és azt is, hogy ki kezd. A játék folyamán a kör mentén óramutató járásával megegyező irányban sorban raknak le egy-egy lapot, de egy \(\displaystyle 2\)-es számú lapot csak akkor rakhatnak le, ha abból a színből az \(\displaystyle 1\)-es már korábban le lett rakva. Akkor nyernek, ha az összes lapot lerakják. Ha valaki a sorra kerülésekor nem tud rakni és még van lap a kezében, veszítenek. Mutassuk meg, hogy a játékosok bármilyen kártya kiosztás esetén tudnak nyerni.

Javasolta: Kocsis Anett és Imolay András (Budapest) a Dürer Verseny feladata alapján

(5 pont)

A beküldési határidő 2025. november 10-én LEJÁRT.

Megoldás. Jelölje \(\displaystyle k\) azon játékosok számát, akik két \(\displaystyle 1\)-es kártyát kaptak (a továbbiakban őket 11-eseknek nevezzük). Mivel ugyanannyi 1-es és 2-es van, ezért ekkor \(\displaystyle k\) olyan játékosnak kell lennie, akik két \(\displaystyle 2\)-es kártyát kaptak (22-esek), míg a maradék \(\displaystyle n-2k\) játékos egy \(\displaystyle 1\)-est és egy \(\displaystyle 2\)-est kapott (12-esek).

Üljenek le a játékosok úgy, hogy először a 11-esek kerüljenek sorra, utána a 12-esek, míg végül a 22-esek (egy-egy csoporton belül a sorrend tetszőleges lehet). A következőkben megmutatjuk, hogy ha ilyen sorrendben ülnek le, akkor (okos választásokkal) le tudják tenni az összes kártyát.

Először a 11-esek tegyenek le egy-egy 1-es kártyát (hogy melyiket a kettő közül, azt később magyarázzuk el). Ezután a 12-esek tegyék le az 1-eseiket. Az első fordulót a 22-esek zárják. Ha ők mindannyian le tudnak tenni egy-egy kártyát, akkor a második fordulóban már nem lehet gond, hiszen mire a második fordulóban először kerül 2-es kártya lerakásra (a sorban először következő 12-es játékosnál), már az összes 1-es kártya le lesz téve.

Tehát csak arra kell figyelnünk, hogy az első fordulóban a 11-esek úgy válasszanak kártyát, hogy az első forduló végén a 22-esek közül mindenki le tudja tenni valamelyik kártyáját.

Készítsünk egy páros gráfot, melynek csúcsainak

• egyik osztálya a 11-es és 12-es halmazának uniója: \(\displaystyle V = \{ v_1, v_2, \ldots, v_{n-k} \}\),
• másik osztálya pedig a 22-es játékosok halmaza: \(\displaystyle W = \{w_1,w_2,\ldots,w_k \}\).

A \(\displaystyle w_i\) csúcsot akkor kötjük össze a \(\displaystyle v_j\) csúccsal, ha a \(\displaystyle w_i\) kezében levő 2-esek közül valamelyiknek az ugyanolyan színű párja \(\displaystyle v_j\) kezében van.

A kapott páros gráfban minden fokszám legfeljebb 2, tehát a gráf utakra és páros körökre bomlik (valójában az utak is mindig páros élből fognak állni, de ennek nincs jelentősége). Hagyjunk el minden második élt a a páros körökből és az utakból alternáló módon, azaz az utaknak az egyik végéről, a köröknek tetszőleges pontjából indulva az első, harmadik, ötödik, stb. éleket megtartva, a második, negyedik, hatodik, stb. éleket elhagyva. Így egy olyan részgráf marad, amelynek minden \(\displaystyle W\)-beli csúcsban pontosan 1, míg minden \(\displaystyle V\)-beli csúcsban legfeljebb 1 a fokszáma, tehát a \(\displaystyle W\) halmazt bepárosítja a \(\displaystyle V\) halmazba.

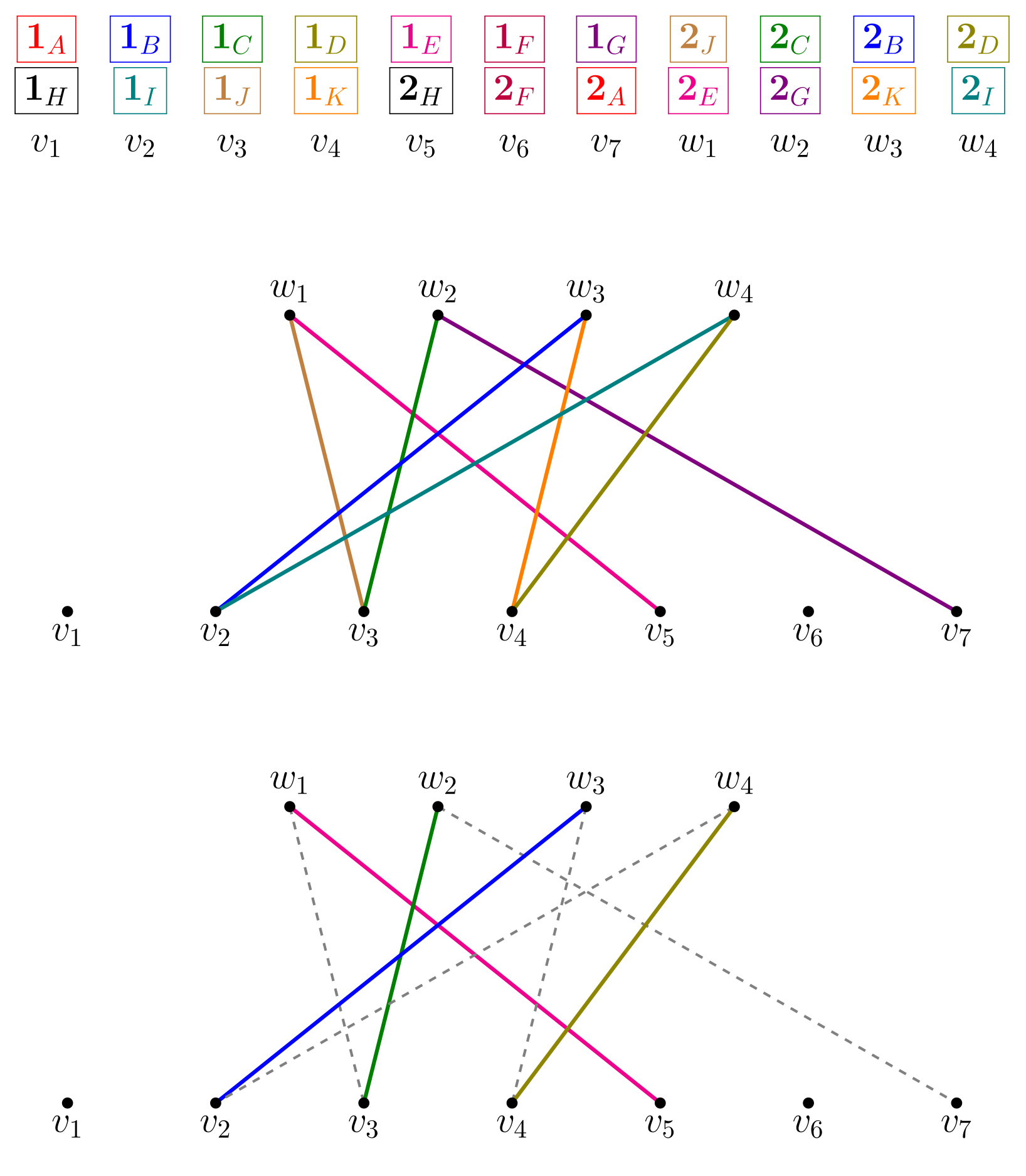
A kapott bepárosítás fogja megadni, hogy miként válasszák ki a 11-es játékosok az elsőként letett kártyájukat. Ha a \(\displaystyle v_i\) jelű 11-es játékos a \(\displaystyle w_j\) jelű 22-esnek a párja a gráfbéli párosítás szerint, akkor \(\displaystyle v_i\)-nek azt a kártyáját kell letennie először, amelyiknek \(\displaystyle w_j\)-nél van az azonos színű párja (esetleg előfordulhat, hogy mindkét \(\displaystyle v_i\)-nél levő kártyának \(\displaystyle w_j\)-nél van a párja – ilyenkor bármelyiket leteheti).

Ezzel garantáljuk, hogy minden 22-es játékos tud lapot tenni az első körben – hiszen mindegyiküknek van egy párja a gráfban, aki biztosítja, hogy legalább az egyik kezükben élevő 2-esnek már le van téve az azonos színű 1-es párja.

Megjegyzés. A páros gráfban a párosítás létezésének bizonyításakor lehet hivatkozni a Kőnig–Hall-tételre is. De mint megmutattuk, igazából nincs szükség a tétel erejére – amennyiben minden fokszám legfeljebb 2, akkor könnyű egy maximális párosítást találni egy páros gráfban.

Megjegyzés. A feladat a Dürer Verseny 2025 februári döntőjén az E kategóriában kitűzött 1b) feladat általánosítása.

Statisztika:

100 dolgozat érkezett.
5 pontot kapott:	73 versenyző.
4 pontot kapott:	14 versenyző.
3 pontot kapott:	6 versenyző.
2 pontot kapott:	2 versenyző.
0 pontot kapott:	2 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	2 dolgozat.

A KöMaL 2025. októberi matematika feladatai