A C. 1269. feladat (2015. január)

C. 1269. Legalább hány oldala van annak a szabályos sokszögnek, amelynél a körülírt kör sugara a beírt kör sugarának legfeljebb 1,1-szerese?

(5 pont)

A beküldési határidő 2015. február 10-én LEJÁRT.

Megoldás. Jelölje a körülírt kör sugarát \(\displaystyle R\), a beírt körét \(\displaystyle r\). Tekintsünk egy, a sokszög egyik oldalának végpontjai és a körök közös középpontja által meghatározott háromszöget. A két sugár által bezárt szöget jelölje \(\displaystyle \alpha\).

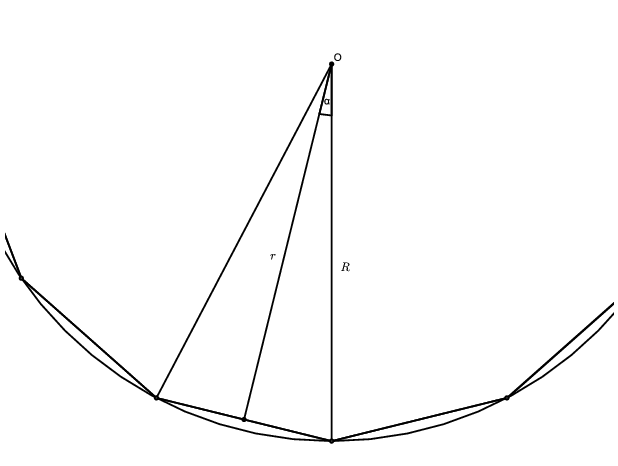
Tudjuk, hogy \(\displaystyle R\leq 1,1r\), amiből \(\displaystyle \frac rR\geq\frac{10}{11}\) következik. Mivel \(\displaystyle \frac rR=\cos\alpha\), a következőt kaptuk: \(\displaystyle \cos\alpha\geq\frac{10}{11}\), amiből \(\displaystyle 0^{\circ}<\alpha<90^{\circ}\) miatt \(\displaystyle \alpha\leq\arccos\frac{10}{11}\) következik.

A szabályos sokszögben \(\displaystyle n\cdot2\alpha=360^{\circ}\), amiből \(\displaystyle \alpha=\frac{360^{\circ}}{2n}\). Ezért \(\displaystyle \frac{360^{\circ}}{2n}\leq\arccos\frac{10}{11}\), és innen \(\displaystyle n\geq\frac{180}{\arccos\frac{10}{11}}\approx7,31\).

Vagyis a sokszög legalább 8 oldalú.

Statisztika:

152 dolgozat érkezett.
5 pontot kapott:	Banczik Zoltán Ádám, Bindics Boldizsár, Bottlik Judit, Bödör András, Bőzsöny András, Di Giovanni András, Egyházi Anna, Erdei Ákos, Erdélyi Janka, Farkas Dóra, Fehér Balázs, Fényes Balázs, Hunyadi Marcell, Jakus Balázs István, Jójárt Alexandra, Klász Viktória, Kocsis Júlia, Kósa Szilárd, Mályusz Attila, Marton Fruzsina, Matusek Márton, Mészáros 01 Viktória, Mihálykó Péter, Mikulás Hanna, Nagy 442 Ádám, Németh 417 Tamás, Pap-Takács Mónika, Sallai Krisztina, Souly Alexandra, Szabó 157 Dániel, Szauer Marcell, Szécsi Adél Lilla, Szemerédi Levente, Szűcs Dorina, Tatai Mihály, Telek Máté László, Tevesz Judit, Tóth Tamás, Török Réka , Varga-Umbrich Eszter, Varjas István Péter, Várkonyi Lídia, Wesniczky Albert.
4 pontot kapott:	69 versenyző.
3 pontot kapott:	24 versenyző.
2 pontot kapott:	5 versenyző.
1 pontot kapott:	6 versenyző.
0 pontot kapott:	5 versenyző.

A KöMaL 2015. januári matematika feladatai