A C. 1276. feladat (2015. február)

C. 1276. Az \(\displaystyle ABCD\) paralelogramma \(\displaystyle AB\), \(\displaystyle BC\), \(\displaystyle CD\), \(\displaystyle DA\) oldalainak belső pontjai rendre \(\displaystyle X\), \(\displaystyle Y\), \(\displaystyle Z\), \(\displaystyle V\), amelyekre fennáll:

\(\displaystyle \frac{AX}{XB}=\frac{BY}{YC}=\frac{CZ}{ZD}=\frac{DV}{VA}=k, \)

ahol a \(\displaystyle k\) egy \(\displaystyle \frac 12\)-nél kisebb pozitív állandó. Mekkora \(\displaystyle k\) értéke, ha az \(\displaystyle XYZV\) négyszög területe az \(\displaystyle ABCD\) paralelogramma területének 68%-a?

(5 pont)

A beküldési határidő 2015. március 10-én LEJÁRT.

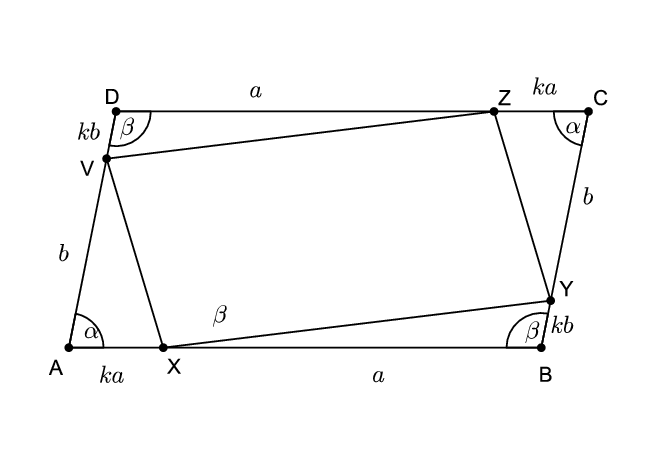
Megoldás. Készítsünk ábrát. Legyen \(\displaystyle XB=a\) és \(\displaystyle YC=b\). Ekkor egyrészt \(\displaystyle AX=ka\) és \(\displaystyle BY=kb\), másrészt - mivel a paralelogramma szemközti oldalai egyenlő hosszúságúak - \(\displaystyle CZ=ka\), \(\displaystyle ZD=a\), \(\displaystyle DV=kb\) és \(\displaystyle VA=b\).

Ha a belső négyszög területe az \(\displaystyle ABCD\) paralelogramma területének 68%-a, akkor a négy levágott háromszög területének összege a paralelogramma területének 32%-ával egyenlő:

\(\displaystyle \frac{t_{XBY}+t_{YZC}+t_{ZDV}+t_{VAX}}{t_{ABCD}}=\frac{32}{100}.\)

Számítsuk ki a négy négyszög területének arányát az \(\displaystyle ABCD\) paralelogramma területéhez külön-külön.

\(\displaystyle \frac{t_{XBY}}{t_{ABCD}}=\frac{t_{XBY}}{2t_{ABC}}=\frac{\frac12\cdot XB\cdot BY\cdot\sin XBY\angle}{2\cdot\frac12\cdot AB\cdot BC\cdot\sin ABC\angle}=\frac{a\cdot kb\sin\beta}{2(ka+a)(kb+b)\sin\beta}=\frac{abk}{2ab(k+1)^2}=\frac{k}{2(k+1)^2}.\)

Ugyanezt az eredményt kapjuk a másik három háromszögre is. A négy háromszögre kapott arányt összeadva:

\(\displaystyle \frac{32}{100}=\frac{t_{XBY}+t_{YZC}+t_{ZDV}+t_{VAX}}{t_{ABCD}}=\frac{2k}{(k+1)^2}.\)

Ezt átalakítva:

\(\displaystyle \frac{2k}{(k+1)^2}=\frac{8}{25},\)

\(\displaystyle 50k=8(k+1)^2,\)

\(\displaystyle 50k=8k^2+16k+8,\)

\(\displaystyle 0=8k^2-34k+8,\)

\(\displaystyle 0=4k^2-17k+4,\)

\(\displaystyle k_{1,2}=\frac{17\pm\sqrt{17^2-4\cdot16}}{8}=\frac{17\pm15}{8},\)

amiből \(\displaystyle k_1=4\) és \(\displaystyle k_2=\frac14\). Mivel most \(\displaystyle k<\frac12\), ezért a megoldás: \(\displaystyle k=\frac14\).

Statisztika:

115 dolgozat érkezett.
5 pontot kapott:	65 versenyző.
4 pontot kapott:	20 versenyző.
3 pontot kapott:	14 versenyző.
2 pontot kapott:	6 versenyző.
1 pontot kapott:	5 versenyző.
0 pontot kapott:	4 versenyző.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2015. februári matematika feladatai