 |
A C. 1277. feladat (2015. február) |
C. 1277. Az \(\displaystyle r^2\) értékétől függően hány megoldása van az
\(\displaystyle x^2 + y^2 =r^2,\)
\(\displaystyle |x| + |y| =2\)
egyenletrendszernek?
(5 pont)
A beküldési határidő 2015. március 10-én LEJÁRT.
Megoldás. Ábrázoljuk a két egyenletet a derékszögű koordináta-rendszerben.
A második egyenlet grafikonja egy négyzet, melynek csúcsai a tengelyeken vannak, az origótól 2 egység távolságra. A négyzet oldalának hossza \(\displaystyle 2\sqrt2\).
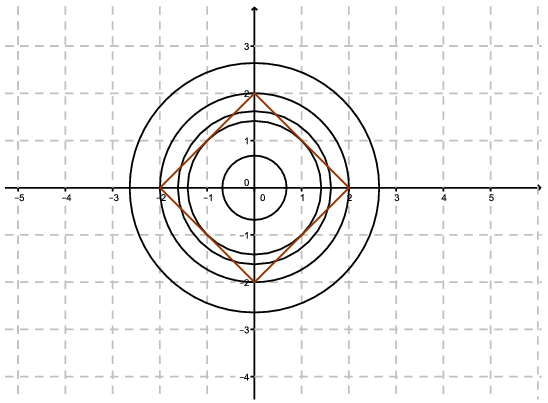
A kör akkor fogja belülről érinteni a négyzetet, ha sugara a négyzet oldalának fele, vagyis ha \(\displaystyle r=\sqrt2\). Ekkor a négy érintési pont adja a négy megoldást.
Ha \(\displaystyle r<\sqrt2\), akkor nincs metszéspont, tehát a megoldások száma 0.
A kör a négyzet köré írható kör lesz, ha \(\displaystyle r=2\), a megoldások száma ekkor is 4.
Ha \(\displaystyle \sqrt2<r<2\), akkor 8 metszéspont van.
Végül, ha \(\displaystyle r>2\) akkor nincs megoldás.
Összegezve: 0 megoldás van \(\displaystyle r^2<2\) és \(\displaystyle r^2>4\) esetén, 4 megoldás van \(\displaystyle r^2=2\) és \(\displaystyle r^2=4\) esetén, és 8 megoldást kapunk, ha \(\displaystyle 2<r^2<4\).
Statisztika:
A KöMaL 2015. februári matematika feladatai
