A C. 1279. feladat (2015. február)

C. 1279. Határozzuk meg azon \(\displaystyle ABCD\) négyzeteket, melyek \(\displaystyle A\) csúcsa a \(\displaystyle (4;-2)\) pont, \(\displaystyle B\) csúcsa rajta van a \(\displaystyle b\colon {(x-5)}^2+ {(y-2)}^2=25\) körön, \(\displaystyle D\) csúcsa pedig a \(\displaystyle d\colon 4x+3y+2=0\) egyenesen.

(5 pont)

A beküldési határidő 2015. március 10-én LEJÁRT.

Megoldás. Ha van egy megfelelő négyzetünk, akkor abban \(\displaystyle DAB\angle=90^{\circ}\), vagyis a \(\displaystyle B\) csúcs \(\displaystyle A\) pont körüli \(\displaystyle \pm90^{\circ}\)-os elforgatottja a \(\displaystyle D\) csúcs.

Forgassuk el tehát a \(\displaystyle b\) kört az \(\displaystyle A\) pont körül. Jelölje a kör középponját \(\displaystyle O\).

I. eset: a forgatás \(\displaystyle 90^{\circ}\)-os. A \(\displaystyle b\) kör \(\displaystyle O\) középpontjának képe a forgatáskor \(\displaystyle O'(0;-1)\), a \(\displaystyle b'\) kör egyenlete pedig \(\displaystyle x^2+(y+1)^2=25\). Ebbe behelyettesítve az egyenes egyenletéből kapott \(\displaystyle y=-\frac43x-\frac23\) kifejezést:

\(\displaystyle x^2+\left(-\frac43x+\frac13\right)^2=25,\)

\(\displaystyle \frac{9+16}{9}x^2-\frac89x+\frac19-25=0,\)

\(\displaystyle 25x^2-8x-224=0,\)

\(\displaystyle x_{1,2}=\frac{8\pm\sqrt{8^2+4\cdot25\cdot224}}{50}=\frac{8\pm\sqrt{22464}}{50},\)

\(\displaystyle x_1=3,1576\) és \(\displaystyle x_2=-2,8376\). Ebből pedig \(\displaystyle y_1=-\frac43\cdot3,1576-\frac23=-4,8768\) és \(\displaystyle y_2=-\frac43\cdot-2,8376-\frac23=3,1168\).

Azt kaptuk, hogy \(\displaystyle D_1(3,1576;-4,8768)\), illetve \(\displaystyle D_2(-2,8376;3,1168)\).

Innen \(\displaystyle \overrightarrow{AD_1}(-0,8424;-2,8768)\), ennek \(\displaystyle -90^{\circ}\)-os elforgatottja \(\displaystyle \overrightarrow{AB_1}(-2,8768;0,8424)\), amiből \(\displaystyle B_1(1,1232;-1,1576)\) és \(\displaystyle C_1(0,2808;-4,0344)\).

Hasonlóan kapjuk, hogy \(\displaystyle \overrightarrow{AD_2}(-6,8376;5,1168)\), amiből \(\displaystyle \overrightarrow{AB_2}(5,1168;6,8376)\), tehát \(\displaystyle B_2(9,1168;4,8376)\) és \(\displaystyle C_2(2,2792;9,9544)\).

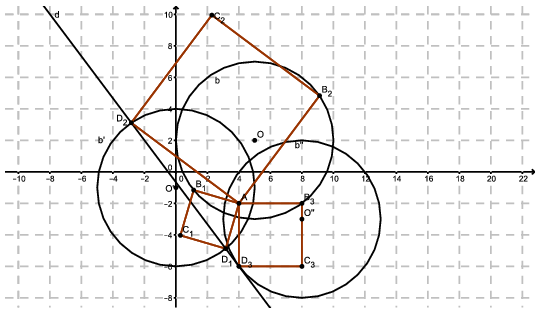
II. eset: a forgatás \(\displaystyle -90^{\circ}\)-os. A \(\displaystyle b\) kör középpontjának képe ekkor \(\displaystyle O''(8;-3)\), a \(\displaystyle b''\) kör egyenlete pedig \(\displaystyle (x-8)^2+(y+3)^2=25\). Ismét behelyettesítve \(\displaystyle y=-\frac43x-\frac23\)-ot:

\(\displaystyle (x-8)^2+\left(-\frac43x+\frac73\right)^2=25,\)

\(\displaystyle 9x^2-144x+576+16x^2-56x+49-225=0,\)

\(\displaystyle 25x^2-200x+400=0,\)

\(\displaystyle 25(x-4)^2=0,\)

vagyis innen \(\displaystyle x=4\), amiből \(\displaystyle y=-\frac43\cdot4-\frac23=-6\). Tehát azt kaptuk, hogy \(\displaystyle D_3(4;-6)\). Ekkor a négyzet oldala 4 egység hosszú, a másik két csúcs koordinátái egyszerűen megkaphatók: \(\displaystyle B_3(8;-2)\) és \(\displaystyle C_3(8;-6)\).

Statisztika:

32 dolgozat érkezett.
5 pontot kapott:	Bottlik Judit, Egyházi Anna, Erdei Ákos, Fülöp Erik, Kasó Ferenc, Kósa Szilárd, Matusek Márton, Sándor Gergely, Varjas István Péter.
4 pontot kapott:	Bereczki Zoltán, Kocsis-Savanya Miklós, Krisztián Jonatán, Mészáros 01 Viktória, Porupsánszki István, Vida Máté Gergely.
3 pontot kapott:	7 versenyző.
2 pontot kapott:	5 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	3 versenyző.

A KöMaL 2015. februári matematika feladatai