A C. 1484. feladat (2018. május)

C. 1484. Az $\displaystyle ABCD$ olyan konvex négyszög, amelynek átlói nem merőlegesek egymásra. Az $\displaystyle A$, $\displaystyle B$, $\displaystyle C$, $\displaystyle D$ csúcsokból az $\displaystyle AC$, illetve $\displaystyle BD$ szakaszokra bocsátott merőlegeseknek létezik a csúcsoktól különböző talppontja, jelölje ezeket rendre $\displaystyle A_1$, $\displaystyle B_1$, $\displaystyle C_1$, $\displaystyle D_1$. Bizonyítsuk be, hogy az ezek által meghatározott négyszög hasonló az eredetihez.

(5 pont)

A beküldési határidő 2018. június 11-én LEJÁRT.

Megoldás. Az átlók nem merőlegesek egymásra, tehát metszéspontjukat $\displaystyle M$-mel jelölve vagy az $\displaystyle AMB\angle$, vagy a $\displaystyle BMC\angle$ hegyesszög. Feltehető, hogy $\displaystyle AMB\angle$ a hegyesszög, ekkor $\displaystyle CMD\angle$ is az, $\displaystyle BMC\angle=DMA\angle$ pedig tompaszög. Így az $\displaystyle AB$ és $\displaystyle CD$ szakaszok Thalész-köre diszjunkt, míg $\displaystyle BC$ és $\displaystyle DA$ Thalész-köre metszi egymást.

Használjuk az 1. ábra jelöléseit.

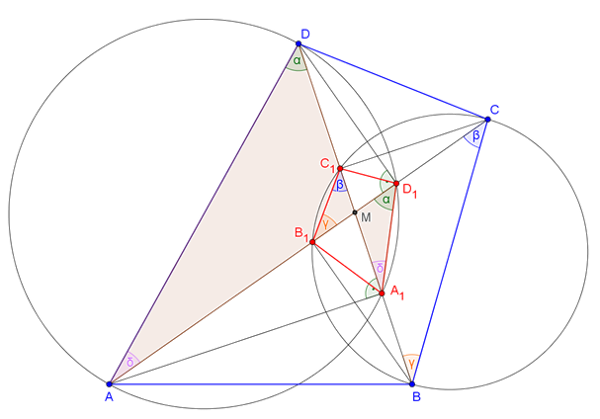
1. ábra

Az $\displaystyle AA_1D$ és $\displaystyle AD_1D$ derékszögű háromszögek, ezért a Thalész-tétel miatt az $\displaystyle AA_1D_1D$ négyszög húrnégyszög. A köré írt körben $\displaystyle ADA_1∡=AD_1A_1∡=α$, azonos ívhez tartozó kerületi szögek. Hasonlóan $\displaystyle DAD_1∡=DA_1D_1∡=δ$. Ugyanígy belátható, hogy a $\displaystyle BB_1C_1C$ négyszög is húrnégyszög és $\displaystyle CBC_1∡=CB_1C_1∡=γ$ és $\displaystyle BCB_1∡=BC_1B_1∡=β$. $\displaystyle AMDΔ≅A_1MD_1Δ$, mert mindhárom szögük egyenlő. Hasonlóan igaz, hogy $\displaystyle BMCΔ≅B_1MC_1Δ$.

Használjuk az 2. ábra jelöléseit.

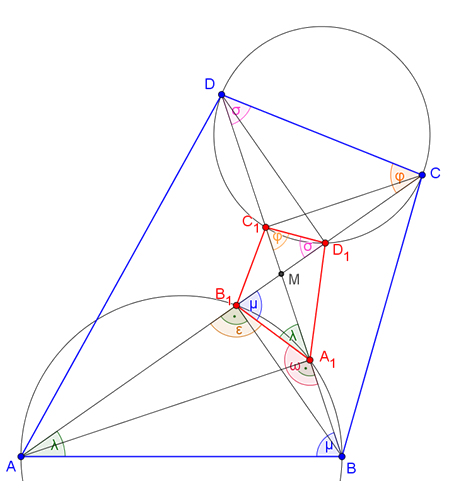
2. ábra

Az $\displaystyle AA_1B$ és $\displaystyle AB_1B$ derékszögű háromszögek, ezért a Thalész-tétel miatt az $\displaystyle ABA_1B_1$ négyszög húrnégyszög. $\displaystyle ABA_1∡+AB_1A_1∡=180°$, mert a húrnégyszög szemközti szögei. $\displaystyle MB_1A_1∡+AB_1A_1∡=180°$, mert kiegészítő szögek. Ezért $\displaystyle ABA_1∡=MB_1A_1∡=μ$. Hasonlóan belátható, hogy $\displaystyle BAB_1∡=MA_1B_1∡=λ$. Ugyanígy belátható, hogy a $\displaystyle CD_1C_1D$ négyszög is húrnégyszög és $\displaystyle DCD_1∡=MC_1D_1∡=φ$, valamint $\displaystyle CDC_1∡=MD_1C_1∡=σ$. $\displaystyle AMBΔ≅A_1MB_1Δ$, mert mindhárom szögük egyenlő. Hasonlóan igaz, hogy $\displaystyle CMDΔ≅C_1MD_1Δ$.

Ezzel beláttuk, hogy az $\displaystyle ABCD$ négyszög minden részháromszöge páronként hasonló az $\displaystyle A_1B_1C_1D_1$ négyszög részháromszögeihez és a szomszédos részháromszögek egy-egy oldala is közös, ezért a hasonlóság arányának is meg kell egyezni. Tehát az $\displaystyle A_1B_1C_1D_1$négyszög hasonló az eredeti $\displaystyle ABCD$ négyszöghöz.

Statisztika:

33 dolgozat érkezett.
5 pontot kapott:	Andó Viola, Biró 424 Ádám, Fodor Marcel, Fonyi Máté Sándor, Gém Viktória, Görcs András, Hordós Adél Zita, Imre Tamás, Kerekes Boldizsár, Kis 194 Károly, Kovács 157 Zita, Markó Gábor, Rátki Luca, Rusvai Miklós, Shuborno Das, Székelyhidi Klára, Williams Hajna.
4 pontot kapott:	Földvári Ádám, Hámori Janka, Kalabay László, Pinke Andrea.
3 pontot kapott:	2 versenyző.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	5 versenyző.
0 pontot kapott:	3 versenyző.

A KöMaL 2018. májusi matematika feladatai