 |
A C. 1629. feladat (2020. október) |
C. 1629. Egy gömb átmegy egy 8 egység élű kocka egyik lapjának négy csúcsán és érinti a szemközti lapot. Határozzuk meg a gömb sugarát.
(Horvát feladat)
(5 pont)
A beküldési határidő 2020. november 10-én LEJÁRT.
Megoldás.
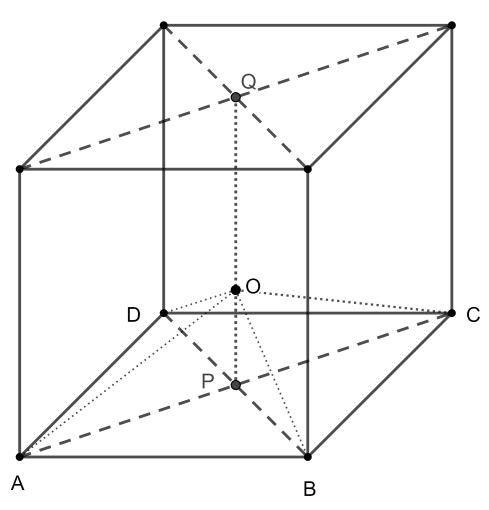
Legyen a lap, aminek négy csúcsán átmegy a gömb \(\displaystyle ABCD\), a lap középpontja \(\displaystyle P\), a szemközti lap középpontja pedig \(\displaystyle Q\), a gömb sugarát pedig jelölje \(\displaystyle r\). Mivel a gömb átmegy az \(\displaystyle A,B,C,D\) pontok mindegyikén, így \(\displaystyle O\) középpontja illeszkedik ezen pontok közül bármely kettő felezőmerőleges síkjára. Ezen síkok metszete a \(\displaystyle P\) pontban az \(\displaystyle ABCD\) síkjára állított merőleges egyenes, vagyis a \(\displaystyle PQ\) egyenes. A gömb \(\displaystyle O\) középpontja tehát a \(\displaystyle PQ\) egyenesre esik. Csak a \(\displaystyle Q\) végpontú, \(\displaystyle P\)-t tartalmazó félegyenesen lehet, hiszen különben \(\displaystyle OQ<OP<OA\) miatt a feltételek nem teljesülhetnének. Tehát \(\displaystyle O\) a \(\displaystyle QP\) félegyenes azon pontja, mely \(\displaystyle r\) távolságra van \(\displaystyle Q\)-tól (hiszen a gömb érinti az \(\displaystyle ABCD\)-vel szemközti lapot, és mivel \(\displaystyle OQ\) merőleges a lapra, ezért az érintési pont \(\displaystyle Q\)): \(\displaystyle QO=r\). Mivel a feltételek szerint \(\displaystyle OA=OB=OC=OD=r\) szintén teljesül, ezért a Pitagorasz-tétel alapján
\(\displaystyle r^2=OA^2=AP^2+PO^2=\frac{1}{4}AC^2+(8-r)^2=\frac{1}{4}(8^2+8^2)+(8-r)^2=r^2-16r+96,\)
amiből \(\displaystyle r=96/16=6\). (A számolás során használtuk, hogy \(\displaystyle PQ=8\), ugyanis \(\displaystyle PQ\) merőleges az \(\displaystyle ABCD\) síkra, és a kocka szemköztes lapjainak távolsága a kocka élhossza.)
Tehát a gömb sugara \(\displaystyle r=6\).
Statisztika:
58 dolgozat érkezett. 5 pontot kapott: Andó Lujza, Baksay Réka, Biró 424 Ádám, Bődi Lili, Dlauchy Miksa, Dobi Dorina Lili, Domján Dorina, Egyházi Hanna, Féger Tamás, Fekete András Albert, Flódung Áron , Golarits Botond, Gombos Gergely , Hámori Szilvia, Horváth 828 Mátyás, Kelemen Anna, Margaritisz Fanni, Molnár Réka, Nagy Vanda Orsolya, Németh László Csaba, Németh Máté Előd, Nyári Péter Ádám, Rátki Gergely, Rokonay Szonja, Schneider Anna, Szabó Csege, Szalanics Tamás, Szirmai Dénes, Téglás Panna, Török Miksa, Tüske Anna, Varga 601 Zalán, Xu Yiling, Zaránd Andris, Zsoldos Péter. 4 pontot kapott: Bana Marcell, Farkas Lili, Fischer Nóra Anna, Fonyi Máté Sándor, Hamar János, Horváth Antal, Katrenák Győző Áron, Kiss 888 Gergely, Németh Kristóf, Schnábel Martin, Sütő Csenge, Toffalini Leonardo, Turai Johanna. 3 pontot kapott: 3 versenyző. 0 pontot kapott: 3 versenyző. Nem versenyszerű: 4 dolgozat.
A KöMaL 2020. októberi matematika feladatai

