A C. 1769. feladat (2023. május)

C. 1769. Az \(\displaystyle ABC\) hegyesszögű háromszög magasságpontja \(\displaystyle M\), az oldalak hosszára \(\displaystyle AB\geq BC \geq CA\) teljesül. Az \(\displaystyle AM\) szakasz felezőmerőlegese az \(\displaystyle AC\) oldalt a \(\displaystyle D\), a \(\displaystyle BM\) szakasz felezőmerőlegese a \(\displaystyle BC\) oldalt az \(\displaystyle E\) pontban metszi. Mekkorák az \(\displaystyle ABC\) háromszög szögei, ha tudjuk, hogy a \(\displaystyle D\), \(\displaystyle M\), \(\displaystyle E\) pontok egy egyenesre illeszkednek?

Javasolta: Bíró Bálint (Eger)

(5 pont)

A beküldési határidő 2023. június 12-én LEJÁRT.

Megoldás. A szokásos jelölést használva legyen \(\displaystyle T_a\) az \(\displaystyle A\)-hoz tartozó magasság, \(\displaystyle T_b\) pedig a \(\displaystyle B\)-hez tartozó magasság talppontja, \(\displaystyle M\) pedig a magasságpont. A háromszög hegyesszögű, tehát a talppontok az oldalaknak belső pontjai, M pedig a háromszögnek belső pontja.

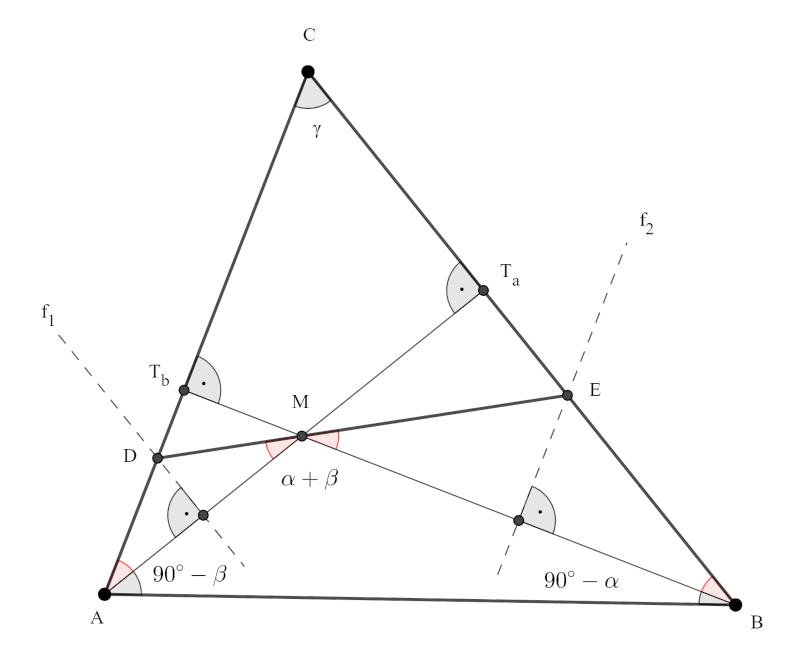
Legyen továbbá az \(\displaystyle AM\) felezőmerőlegese \(\displaystyle f_1\), a \(\displaystyle BM\) felezőmerőlegese pedig \(\displaystyle f_2\). Ekkor a \(\displaystyle CAT_a\), a \(\displaystyle T_{a}AB\), a \(\displaystyle CT_{b}B\) és a \(\displaystyle T_{b}AB\) derékszögű háromszögek szögeire, az \(\displaystyle AMD\) és az \(\displaystyle MBE\) egyenlő szárú háromszögek szögeire, valamint az \(\displaystyle ABM\) háromszög szögeire az alábbi összefüggések igazak:

\(\displaystyle DMA\sphericalangle=DAM\sphericalangle=90^{\circ}-\gamma=MBE \sphericalangle=EMB\sphericalangle,\)

\(\displaystyle MAB \sphericalangle =90^{\circ}-\beta,\)

\(\displaystyle MBA=\sphericalangle=90^{\circ}-\alpha,\)

\(\displaystyle AMB\sphericalangle=\alpha+\beta.\)

Ezeket az összefüggéseket az ábrán is jelöltük. A \(\displaystyle D\), az \(\displaystyle M\) és az \(\displaystyle E\) pontok pontosan akkor vannak egy egyenesen, ha \(\displaystyle DMA\sphericalangle+AMB\sphericalangle+EMB\sphericalangle=180^{\circ}\), vagyis, ha \(\displaystyle (90^{\circ}-\gamma)+(\alpha+\beta)+(90^{\circ}-\gamma)=180^{\circ}\). Ezt rendezve azt kapjuk, hogy \(\displaystyle 2\gamma=\alpha+\beta\). Tudjuk, hogy \(\displaystyle \alpha+\beta+\gamma=180^{\circ}\), tehát \(\displaystyle 3\gamma=180^{\circ}\), vagyis \(\displaystyle \gamma=60^{\circ}\). A feladat feltételének értelmében az oldalak nagyság szerinti sorrendje: \(\displaystyle AB\geq BC \geq CA\), ezért a velük szemközti szögek nagyság szerinti sorrendje is ugyanez, tehát \(\displaystyle \gamma\geq \alpha \geq \beta\). Ezt összevetve azzal, hogy \(\displaystyle \alpha+\beta=120^{\circ}\) azt kapjuk, hogy \(\displaystyle \alpha=\beta=\gamma=60^{\circ}\).

Statisztika:

56 dolgozat érkezett.
5 pontot kapott:	Iván Máté Domonkos, Sütő Áron, Ujpál Bálint, Varga Dániel 829.
4 pontot kapott:	Aaishipragya Kahaly, Baksa Anna, Beke Botond, Blaskovics Ádám, Braun Zsófia, Duzmath Izabella, Fiser 234 Boldizsár, Hauser Márton, Hosszu Noel, Illés Dóra, Jurácsik Marcell, Kerekes András, Keszthelyi Eszter, Klement Tamás, Kővágó Edit Gréta, Márfai Dóra, Mészáros Anna Veronika, Mező Levente, Monoczki Máté, Nagypál Katóca, Pánovics Máté, Papp Zsófia, Richlik Márton, Schneider Dávid, Sipeki Márton, Somogyi Dóra, Szabó Donát, Szittyai Anna, Teveli Jakab, Török Eszter Júlia, Végh Lilian, Volford Barnabás, Waldhauser Miklós, Wodala Gréta Klára.
3 pontot kapott:	3 versenyző.
2 pontot kapott:	5 versenyző.
0 pontot kapott:	3 versenyző.
Nem versenyszerű:	2 dolgozat.

A KöMaL 2023. májusi matematika feladatai