 |
A C. 1789. feladat (2023. december) |
C. 1789. Egy teknőc \(\displaystyle 14\) egységnyi utat jár be a síkon, lépésenként egységnyi szakaszokat megtéve. Minden megtett lépést követően elfordul: ha az előző lépés sorszáma páratlan volt, akkor \(\displaystyle 60^{\circ}\)-kal, ha páros, akkor \(\displaystyle 90^{\circ}\)-kal, továbbá a \(\displaystyle 3.\), \(\displaystyle 5.\), \(\displaystyle 8.\) és \(\displaystyle 12.\) lépést követően jobbra, minden más esetben balra. Mutassuk meg, hogy a teknőc
\(\displaystyle a)\) a \(\displaystyle 14.\) lépés megtételével visszajut a kezdőpontjába és a kezdő irányába,
\(\displaystyle b)\) adjuk meg algebrai alakban a teknőc által körüljárt területet.
Javasolta: Szilassi Lajos (Szeged)
(5 pont)
A beküldési határidő 2024. január 10-én LEJÁRT.
Megoldás. Az a) feladatrész megoldásához ábrát készítünk. Ezen legyen a teknőc útvonalának kezdőpontja \(\displaystyle A\), az útvonal további pontjait jelöljük rendre a \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle D\), \(\displaystyle E\), \(\displaystyle F\), \(\displaystyle G\), \(\displaystyle H\), \(\displaystyle I\), \(\displaystyle J\), \(\displaystyle K\), \(\displaystyle L\), \(\displaystyle M\), \(\displaystyle N\) betűkkel, a teknőc egy-egy lépését pedig egy-egy megfelelő egységvektorral. Az óramutató járásával ellentétes irányú (balra történő) elfordulások szögeit pozitív előjellel ellátva az óramutató járásával megegyező (jobbra történő) elfordulások szöge negatív lesz.
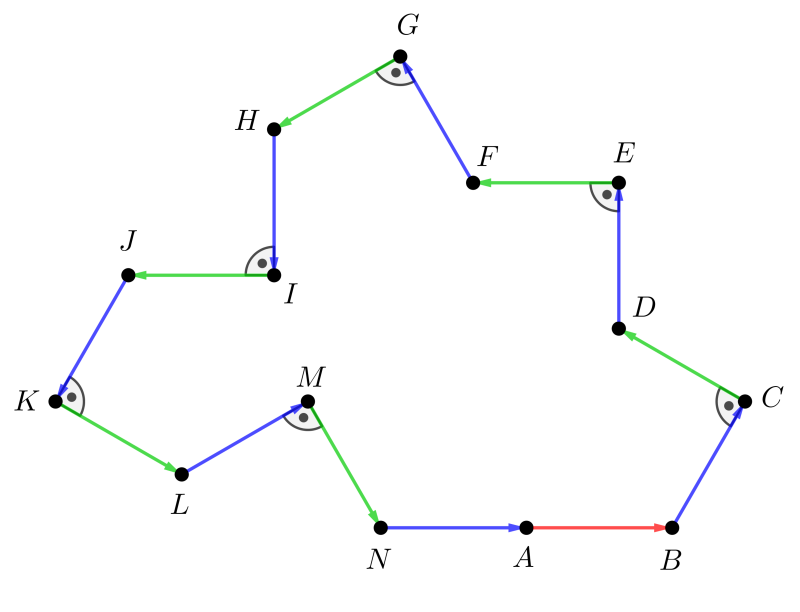
1. ábra
Egyszerű számolással igazolhatjuk, hogy a szögelfordulások előjeles összege \(\displaystyle 360^{\circ}\), ez pontosan azt jelenti, hogy az első és az utolsó egységvektor egyirányú.
Az utolsó egységvektor kezdőpontja \(\displaystyle N\), igazolni fogjuk, hogy a végpontja éppen \(\displaystyle A\). Egyszerűen látható, hogy minden egységvektornak az ellentett vektora is szerepel az ábrán.
Ezek a vektorpárok:
\(\displaystyle \overrightarrow{AB},\qquad \overrightarrow{EF};\)
\(\displaystyle \overrightarrow{BC},\qquad \overrightarrow{JK};\)
\(\displaystyle \overrightarrow{CD},\qquad \overrightarrow{KL};\)
\(\displaystyle \overrightarrow{DE},\qquad \overrightarrow{HI};\)
\(\displaystyle \overrightarrow{FG},\qquad \overrightarrow{MN};\)
\(\displaystyle \overrightarrow{GH},\qquad \overrightarrow{LM};\)
végül pedig az \(\displaystyle \overrightarrow{IJ}\) egységvektor ellentett vektora éppen az \(\displaystyle N\) kezdőpontú egységvektor. Eszerint a teknőc lépéseinek megfelelő egységvektorok összege nullvektor, ami csakis úgy lehetséges, hogy az utolsó egységvektor végpontja az \(\displaystyle A\) pont.
b) A teknőc lépéseivel az 1. ábra szerint egy zárt sokszöget járt körbe. A zárt sokszög területének kiszámításához átalakítjuk az előző ábrát: a sokszögből levágjuk a \(\displaystyle BCD\), \(\displaystyle DEF\), \(\displaystyle FGH\), \(\displaystyle JKL\) egyenlő szárú derékszögű háromszögeket és azok közül kettőt a \(\displaystyle HIJ\), \(\displaystyle LMN\) egyenlő szárú derékszögű háromszögek helyére illesztünk, a maradék kettőt pedig befogóikkal az \(\displaystyle NA\), illetve \(\displaystyle AB\) szakaszokra, úgy, hogy az így létrejövő \(\displaystyle P\) pont a zárt sokszög külső pontja legyen. Végül a \(\displaystyle P\) pontot \(\displaystyle NB\)-re tükrözve a \(\displaystyle Q\) pontot kapjuk.
Tekintsük az így készített ábrát.
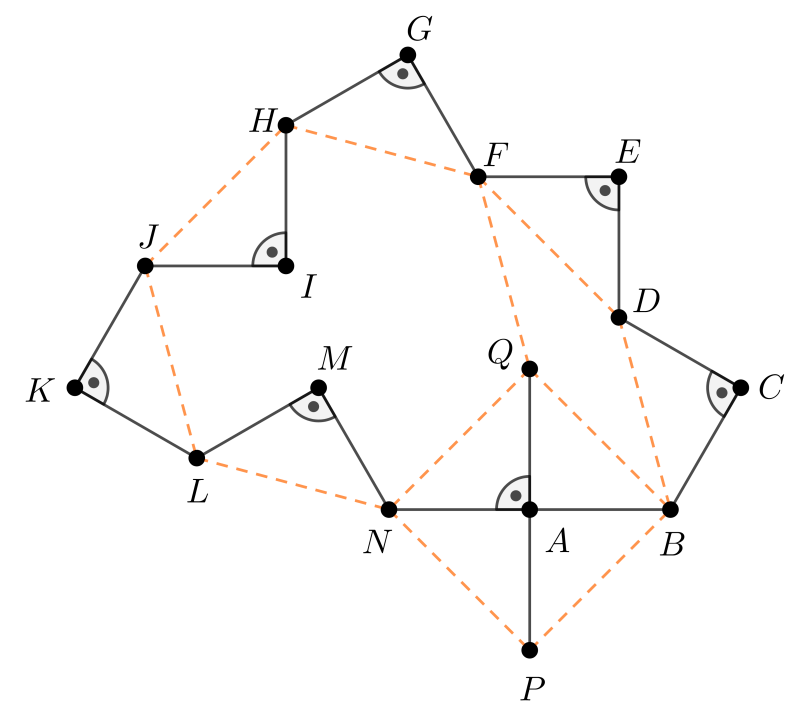
2. ábra
Az előző műveletek eredényeképpen a teknőc lépéseivel körbezárt sokszög területe a \(\displaystyle QFHJLN\) hatszög, a \(\displaystyle BDFQ\) és az \(\displaystyle NPBQ\) négyszög területének összegével egyenlő.
A hatszög oldalai egyenlő hosszúak, hiszen minden oldalhossza \(\displaystyle \sqrt{2}\)-vel egyenlő, a teknőc elfordulási szögei miatt a hatszög minden szöge \(\displaystyle 120^{\circ}\)-os, tehát \(\displaystyle QFHJLN\) szabályos hatszög, ezért területe
| \(\displaystyle (1)\) | \(\displaystyle \displaystyle{T_{QFHJLN}=6\cdot \frac{\big(\sqrt{2}\big)^2\cdot \sqrt{3}}{4}=3\cdot \sqrt{3}}.\) |
Az \(\displaystyle NPBQ\) négyszög négyzet, hiszen oldalaira teljesül, hogy \(\displaystyle NP=PB=BQ=QN=\sqrt{2}\), illetve \(\displaystyle QNP\sphericalangle=90^{\circ}\), ezért a területe
| \(\displaystyle (2)\) | \(\displaystyle \displaystyle{T_{NPBQ}=\big(\sqrt{2}\big)^2=2}.\) |
Végül \(\displaystyle BD=DF=FQ=QB=\sqrt{2}\), és a teknőc szögelfordulásaiból láthatóan a \(\displaystyle BDFQ\) négyszög szögei a \(\displaystyle B\), \(\displaystyle F\) csúcsoknál \(\displaystyle 30^{\circ}\)-osak, a \(\displaystyle D\), \(\displaystyle Q\) csúcsoknál \(\displaystyle 150^{\circ}\)-osak, így a négyszög rombusz, területe pedig
| \(\displaystyle (3)\) | \(\displaystyle \displaystyle{T_{BDFQ}=\sqrt{2}\cdot \sqrt{2}\cdot \sin 30^{\circ}=1}.\) |
A teknőc által körüljárt terület nagysága (1)-(2)-(3) alapján tehát:
\(\displaystyle T_{QFHJLN}+T_{NPBQ}+T_{BDFQ}=3\cdot \sqrt{3}+3.\)
Statisztika:
143 dolgozat érkezett. 5 pontot kapott: Auer Sára, Balogh Péter, Barna Márton, Beinschroth Máté, Blaskovics Ádám, Blaskovics Bálint, Danka Emma, Gyuricsek Ákos, Inokai Ádám, Iván Máté Domonkos, Komlósdi Sára, Márfai Dóra, Masa Barnabás, Mikó Hédi Irma, Molnár-Sáska Tamás, Monoczki Máté, Pánovics Máté, Pázmándi Renáta , Petró Péter, Sebők Violetta Írisz, Sipos Márton, Szabó 926 Bálint, Szabó 926 Bence, Szabó Donát, Tóth 207 Bence, Török Eszter Júlia, Ujpál Bálint, Volford Barnabás, Wodala Gréta Klára, Žigo Boglárka, Zólyomi Csongor. 4 pontot kapott: Aaishipragya Kahaly, Baksa Anna, Bencze Mátyás, Bérczes Botond, Budai Máté, Csáki Botond Benjámin, Domján István, Harmincz Sára, Hauser Márton, Károlyi József, Máté Kristóf, Németh Hanna Júlia , Válek Péter. 3 pontot kapott: 4 versenyző. 2 pontot kapott: 34 versenyző. 1 pontot kapott: 20 versenyző. 0 pontot kapott: 22 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 8 dolgozat.
A KöMaL 2023. decemberi matematika feladatai

