 |
A C. 1847. feladat (2025. február) |
C. 1847. Az \(\displaystyle ABCD\) négyzet \(\displaystyle AD\) oldalán válasszuk ki úgy a \(\displaystyle P\) pontot, hogy \(\displaystyle CPA\sphericalangle=105^{\circ}\) legyen. A \(\displaystyle CP\) egyenesre az \(\displaystyle A\) pontból bocsássunk merőlegest, amelynek talppontját jelölje \(\displaystyle Q\). Határozzuk meg az \(\displaystyle ABQ\) és az \(\displaystyle ACP\) háromszögek területe arányának pontos értékét.
Javasolta: Bíró Bálint, Eger
(5 pont)
A beküldési határidő 2025. március 10-én LEJÁRT.
Megoldás. Tekintsük az alábbi ábrát.
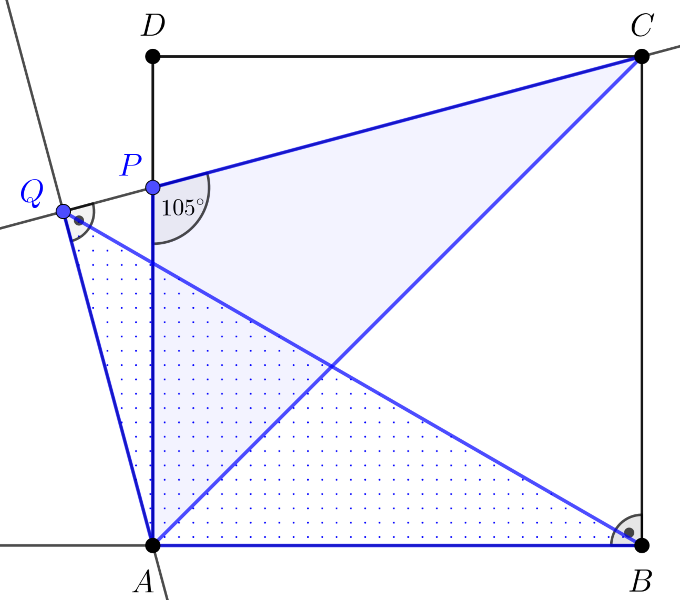
Legyen az \(\displaystyle ABCD\) négyzet oldalhossza egységnyi. A feltételek miatt \(\displaystyle DPC\sphericalangle=75^{\circ}\), illetve \(\displaystyle PCD\sphericalangle=15^{\circ}\) ezért \(\displaystyle PCA\sphericalangle=30^{\circ}\).
A trigonometrikus területképlet segítségével az \(\displaystyle ACP\) háromszög területe
| \(\displaystyle (1)\) | \(\displaystyle \displaystyle{t_{ACP}=\frac{PC\cdot AC\cdot \sin30^{\circ}}{2}}.\) |
A \(\displaystyle PCD\) háromszögben \(\displaystyle \displaystyle{\sin 75^{\circ}=\frac{CD}{PC}=\frac{1}{PC}}\).
Az ismert
\(\displaystyle \displaystyle{\sin75^{\circ}=\sin\big(45^{\circ}+30^{\circ}\big)=\sin45^{\circ}\cdot \cos30^{\circ}+\cos45^{\circ}\cdot\sin30^{\circ}=\frac{\sqrt{2}}{2}\cdot\frac{\sqrt{3}}{2}+\frac{\sqrt{2}}{2}\cdot\frac{1}{2}}\)
trigonometrikus addíciós azonosságból kapjuk, hogy
\(\displaystyle \displaystyle{\sin 75^{\circ}=\frac{\sqrt{2}}{4}\cdot \Big(\sqrt{3}+1\Big)}.\)
Ezért \(\displaystyle \displaystyle{\frac{\sqrt{2}}{4}\cdot\Big(\sqrt{3}+1\Big)=\frac{1}{PC}}\), ahonnan egyszerű számolással kapjuk, hogy
| \(\displaystyle (2)\) | \(\displaystyle PC=\sqrt{2}\cdot \Big(\sqrt{3}-1\Big).\) |
A (2) eredményt és az \(\displaystyle AC=\sqrt{2}\) értéket (1)-be írva és felhasználva, hogy \(\displaystyle \displaystyle{\sin30^{\circ}=\frac{1}{2}}\),
| \(\displaystyle (3)\) | \(\displaystyle \displaystyle{t_{ACP}=\frac{\sqrt{3}-1}{2}}.\) |
Az \(\displaystyle ACQ\) derékszögű háromszögben \(\displaystyle ACQ\sphericalangle=30^{\circ}\), ezért ez a háromszög egy szabályos háromszög fele, így tehát \(\displaystyle \displaystyle{AQ=\frac{AC}{2}=\frac{\sqrt{2}}{2}}\).
Az ábrát tanulmányozva egyszerűen beláthatjuk, hogy \(\displaystyle QAP\sphericalangle=15^{\circ}\), ebből azonnal adódik, hogy \(\displaystyle QAB\sphericalangle=105^{\circ}\), emiatt az \(\displaystyle ABQ\) háromszög területe:
| \(\displaystyle (4)\) | \(\displaystyle t_{ABQ}=\frac{AQ\cdot AB\cdot\sin105^{\circ}}{2}.\) |
Mivel \(\displaystyle \displaystyle{AQ=\frac{\sqrt{2}}{2}}\) és \(\displaystyle AB=1\), valamint egy trigonometrikus azonosság szerint \(\displaystyle \displaystyle{\sin105^{\circ}=\sin75^{\circ}=\frac{\sqrt{2}}{4}\cdot \Big(\sqrt{3}+1\Big)}\), így a (4)-be való helyettesítés és a műveletek elvégzése után
| \(\displaystyle (5)\) | \(\displaystyle \displaystyle{t_{ABQ}=\frac{\sqrt{3}+1}{8}}.\) |
(5) és (3) megfelelő oldalait egymással osztva kapjuk, egyszerűsítés és gyöktelenítés után
\(\displaystyle \displaystyle{\frac{t_{ABQ}}{t_{ACP}}=\frac{\sqrt{3}+2}{4}}.\)
Statisztika:
A C. 1847. feladat értékelése még nem fejeződött be.
A KöMaL 2025. februári matematika feladatai