 Problem C. 1847. (February 2025)
Problem C. 1847. (February 2025)
C. 1847. Let point \(\displaystyle P\) be chosen on side \(\displaystyle AD\) of square \(\displaystyle ABCD\) such that \(\displaystyle \angle CPA=105^{\circ}\). Let \(\displaystyle Q\) be the foot of the perpendicular from \(\displaystyle A\) to \(\displaystyle CP\). Find the exact value of the ratio of the areas of triangles \(\displaystyle ABQ\) and \(\displaystyle ACP\).
Proposed by: Bálint Bíró, Eger
(5 pont)
Deadline expired on March 10, 2025.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Tekintsük az alábbi ábrát.
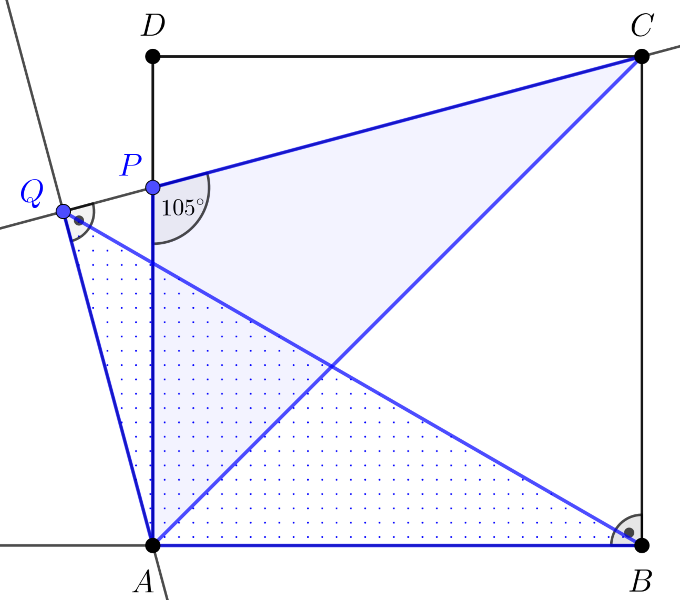
Legyen az \(\displaystyle ABCD\) négyzet oldalhossza egységnyi. A feltételek miatt \(\displaystyle DPC\sphericalangle=75^{\circ}\), illetve \(\displaystyle PCD\sphericalangle=15^{\circ}\), ezért \(\displaystyle PCA\sphericalangle=30^{\circ}\).
A trigonometrikus területképlet segítségével az \(\displaystyle ACP\) háromszög területe
| \(\displaystyle (1)\) | \(\displaystyle \displaystyle{t_{ACP}=\frac{PC\cdot AC\cdot \sin30^{\circ}}{2}}.\) |
A \(\displaystyle PCD\) háromszögben \(\displaystyle \displaystyle{\sin 75^{\circ}=\frac{CD}{PC}=\frac{1}{PC}}\).
Az ismert
\(\displaystyle \displaystyle{\sin75^{\circ}=\sin\big(45^{\circ}+30^{\circ}\big)=\sin45^{\circ}\cdot \cos30^{\circ}+\cos45^{\circ}\cdot\sin30^{\circ}=\frac{\sqrt{2}}{2}\cdot\frac{\sqrt{3}}{2}+\frac{\sqrt{2}}{2}\cdot\frac{1}{2}}\)
trigonometrikus addíciós azonosságból kapjuk, hogy
\(\displaystyle \displaystyle{\sin 75^{\circ}=\frac{\sqrt{2}}{4}\cdot \Big(\sqrt{3}+1\Big)}.\)
Ezért \(\displaystyle \displaystyle{\frac{\sqrt{2}}{4}\cdot\Big(\sqrt{3}+1\Big)=\frac{1}{PC}}\), ahonnan egyszerű számolással kapjuk, hogy
| \(\displaystyle (2)\) | \(\displaystyle PC=\sqrt{2}\cdot \Big(\sqrt{3}-1\Big).\) |
A (2) eredményt és az \(\displaystyle AC=\sqrt{2}\) értéket (1)-be írva és felhasználva, hogy \(\displaystyle \displaystyle{\sin30^{\circ}=\frac{1}{2}}\),
| \(\displaystyle (3)\) | \(\displaystyle \displaystyle{t_{ACP}=\frac{\sqrt{3}-1}{2}}.\) |
Az \(\displaystyle ACQ\) derékszögű háromszögben \(\displaystyle ACQ\sphericalangle=30^{\circ}\), ezért ez a háromszög egy szabályos háromszög fele, így tehát \(\displaystyle \displaystyle{AQ=\frac{AC}{2}=\frac{\sqrt{2}}{2}}\).
Az ábrát tanulmányozva egyszerűen beláthatjuk, hogy \(\displaystyle QAP\sphericalangle=15^{\circ}\), ebből azonnal adódik, hogy \(\displaystyle QAB\sphericalangle=105^{\circ}\), emiatt az \(\displaystyle ABQ\) háromszög területe:
| \(\displaystyle (4)\) | \(\displaystyle t_{ABQ}=\frac{AQ\cdot AB\cdot\sin105^{\circ}}{2}.\) |
Mivel \(\displaystyle \displaystyle{AQ=\frac{\sqrt{2}}{2}}\) és \(\displaystyle AB=1\), valamint egy trigonometrikus azonosság szerint \(\displaystyle \displaystyle{\sin105^{\circ}=\sin75^{\circ}=\frac{\sqrt{2}}{4}\cdot \Big(\sqrt{3}+1\Big)}\), így a (4)-be való helyettesítés és a műveletek elvégzése után
| \(\displaystyle (5)\) | \(\displaystyle \displaystyle{t_{ABQ}=\frac{\sqrt{3}+1}{8}}.\) |
(5) és (3) megfelelő oldalait egymással osztva kapjuk, egyszerűsítés és gyöktelenítés után
\(\displaystyle \displaystyle{\frac{t_{ABQ}}{t_{ACP}}=\frac{\sqrt{3}+2}{4}}.\)
Statistics:
34 students sent a solution. 5 points: Albert Luca Liliána, Bán Kincső Panni, Bencze Mátyás, Budai Máté, Farkas András, Hetyei Dániel, Iván Máté Domonkos, Király Zsuzsanna , Kókai Ákos, Kulcsár Anna Zita, Masa Barnabás, Molnár Lili, Monoczki Máté, Móricz Zsombor, Pink István, Rózsa Zsombor, Száva András, Wolf Erik. 4 points: Farkas Máté, Pánovics Máté. 3 points: 3 students. 2 points: 2 students. 1 point: 2 students. 0 point: 3 students.
Problems in Mathematics of KöMaL, February 2025
