 |
A C. 1849. feladat (2025. március) |
C. 1849. Az \(\displaystyle ABCD\) konvex négyszög \(\displaystyle AB\) oldalának negyedelőpontjai az \(\displaystyle A\) ponttól a \(\displaystyle B\) felé haladva rendre \(\displaystyle N_1\), \(\displaystyle N_2\), \(\displaystyle N_3\), a \(\displaystyle DC\) oldal negyedelőpontjai a \(\displaystyle D\) ponttól a \(\displaystyle C\) felé haladva rendre \(\displaystyle M_1\), \(\displaystyle M_2\), \(\displaystyle M_3\).
Hosszabbítsuk meg az \(\displaystyle AB\) oldalt a \(\displaystyle B\) ponton túl az \(\displaystyle AB\) oldal hosszának negyedrészével, így kapjuk az \(\displaystyle N_4\) pontot. Hasonlóképpen hosszabbítsuk meg a \(\displaystyle DC\) oldalt a \(\displaystyle C\) ponton túl a \(\displaystyle DC\) oldal hosszának negyedrészével, így az \(\displaystyle M_4\) pontot kapjuk.
Határozzuk meg az \(\displaystyle ABCD\) négyszög területét, ha tudjuk, hogy az \(\displaystyle AN_1M_1D\), illetve \(\displaystyle BN_4M_4C\) négyszögek területe \(\displaystyle 8\), illetve \(\displaystyle 10\) területegység.
Bíró Bálint, Eger
(5 pont)
A beküldési határidő 2025. április 10-én LEJÁRT.
Megoldás. Először igazolunk egy segédtételt. Ehhez tekintsük az 1. ábrát, amelyen megrajzoltuk a \(\displaystyle PSUZ\) konvex négyszöget és a \(\displaystyle PS\), illetve \(\displaystyle UZ\) oldalainak \(\displaystyle Q\), \(\displaystyle R\), illetve \(\displaystyle V\), \(\displaystyle X\) harmadolópontjait. Azt fogjuk bizonyítani, hogy \(\displaystyle \displaystyle{T_{QRVX}=\frac{T_{PQXZ}+T_{RSUV}}{2}}\), azaz a középső négyszög területe a másik két négyszög területének számtani közepe.
1. ábra
Az ábra jelöléseit használva \(\displaystyle T_{QVX}=t_2\), hiszen \(\displaystyle QX\) a \(\displaystyle QVZ\) háromszög súlyvonala és a súlyvonal felezi a háromszög területét.
Hasonlóan kapjuk, hogy \(\displaystyle T_{SVR}=t_3\), mivel \(\displaystyle VR\) az \(\displaystyle SVQ\) háromszög súlyvonala. Ezzel
| \(\displaystyle (1)\) | \(\displaystyle T_{PSUZ}=t_1+2t_2+2t_3+t_4.\) |
A \(\displaystyle PSZ\) háromszög területe \(\displaystyle 3t_1\), mert a \(\displaystyle PQZ, QRZ\) és \(\displaystyle RSZ\) háromszögek \(\displaystyle Z\) csúcsa közös, ezért a \(\displaystyle PQ=QR=RS\) oldalakhoz tartozó magasságuk is egyenlő. Hasonlóképpen adódik, hogy az \(\displaystyle UZS\) háromszög területe \(\displaystyle 3t_4\), ezzel pedig:
| \(\displaystyle (2)\) | \(\displaystyle T_{PSUZ}=3t_1+3t_4.\) |
Az (1) és (2) összefüggésekből egyszerűen adódik, hogy \(\displaystyle t_2+t_3=t_1+t_4\), ebből pedig \(\displaystyle 2t_2+2t_3=t_1+t_2+t_3+t_4=T_{PQXZ}+T_{RSUV}\), vagyis
| \(\displaystyle (3)\) | \(\displaystyle \displaystyle{t_2+t_3=T_{QRVX}=\frac{T_{PQXZ}+T_{RSUV}}{2}},\) |
és ezzel a segédtételt igazoltuk.
Ábrázoljuk most a feladatban szereplő \(\displaystyle ABCD\) négyszöget és a megfelelő osztópontokat úgy, hogy a rajzon feltüntetjük az egyes négyszögek területét is (2. ábra).
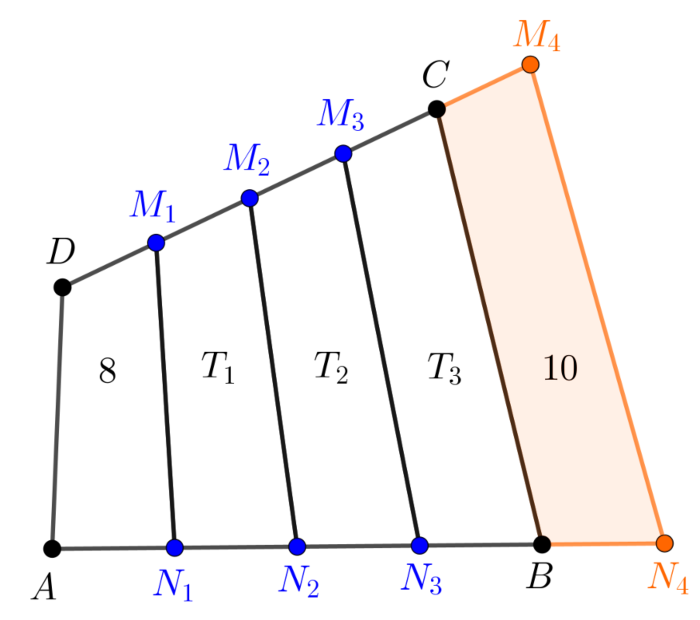
2. ábra
Az ábra szerint
| \(\displaystyle (4)\) | \(\displaystyle T_{ABCD}=8+T_1+T_2+T_3.\) |
Alkalmazzuk többször a segédtételt:
| \(\displaystyle (5)\) | \(\displaystyle \displaystyle{T_1=\frac{8+T_2}{2};\quad T_2=\frac{T_1+T_3}{2};\quad T_3=\frac{T_2+10}{2}}.\) |
Az első és a harmadik egyenlőségből a \(\displaystyle T_1\) és \(\displaystyle T_3\) kifejezését a középsőbe helyettesítve az egyenlet rendezése után kapjuk, hogy
\(\displaystyle T_2=9,\)
amelyből behelyettesítéssel adódik, hogy
\(\displaystyle \displaystyle{T_1=\frac{17}{2};\quad T_3=\frac{19}{2}}.\)
Eredményeinkből (4) alapján kapjuk az \(\displaystyle ABCD\) négyszög területét:
\(\displaystyle T_{ABCD}=35.\)
Ezzel a megoldást befejeztük.
Megjegyzések. 1) A konstrukció és a bizonyított segédtétel következménye, hogy \(\displaystyle 8<T_1<T_2<T_3<10\), és ezért a \(\displaystyle BN_4\) és \(\displaystyle CM_4\) szakaszoknak nem lehet közös pontja.
2) A segédtételből az is következik, hogy például az \(\displaystyle N_1N_2M_2M_1\) négyszög \(\displaystyle T_1\) területe az \(\displaystyle AN_3M_3D\) négyszög területének harmadrésze, és az is, hogy az \(\displaystyle N_2N_3M_3M_2\) négyszög \(\displaystyle T_2\) területe az \(\displaystyle AN_4M_4D\) négyszög területének ötödrésze.
Statisztika:
A C. 1849. feladat értékelése még nem fejeződött be.
A KöMaL 2025. márciusi matematika feladatai