 |
A C. 1854. feladat (2025. április) |
C. 1854. A \(\displaystyle k_1\) és a \(\displaystyle k_2\) kör az \(\displaystyle A\) és \(\displaystyle B\) pontban metszi egymást úgy, hogy a \(\displaystyle k_2\) kör áthalad a \(\displaystyle k_1\) kör \(\displaystyle K\) középpontján. Válasszuk ki a \(\displaystyle k_2\) körvonalnak egy \(\displaystyle S\) pontját úgy, hogy \(\displaystyle S\) közelebb legyen \(\displaystyle A\)-hoz, mint \(\displaystyle B\)-hez és ne essen a \(\displaystyle k_1\) belsejébe. A \(\displaystyle BS\) egyenes és \(\displaystyle k_1\) második metszéspontja legyen \(\displaystyle D\), az \(\displaystyle AD\) egyenes a \(\displaystyle k_2\) kört másodszor a \(\displaystyle T\) pontban metszi. Igazoljuk, hogy \(\displaystyle KT\) merőleges \(\displaystyle BS\)-re.
görög versenyfeladat
(5 pont)
A beküldési határidő 2025. május 12-én LEJÁRT.
Megoldás. Tekintsük a feltételeknek megfelelően készített alábbi ábrát, amelyen a
\(\displaystyle DAK\sphericalangle=\alpha;\quad KBD\sphericalangle=\beta;\quad TDB\sphericalangle=\delta;\quad KTD\sphericalangle=\tau\)
szögeket jelöltük meg.
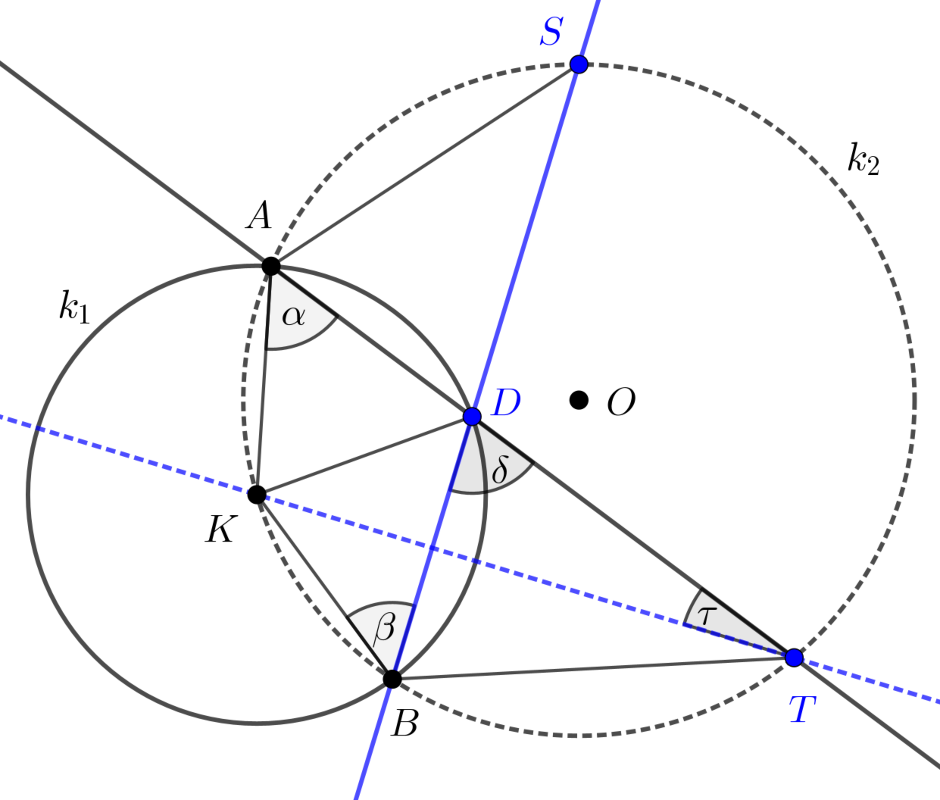
Mivel \(\displaystyle KA\), \(\displaystyle KB\) és \(\displaystyle KD\) a \(\displaystyle k_1\) kör sugarai, ezért a \(\displaystyle DAK\) és \(\displaystyle BDK\) egyenlő szárú háromszögek és így
| \(\displaystyle (1)\) | \(\displaystyle KDA\sphericalangle=\alpha;\quad BDK\sphericalangle=\beta.\) |
A \(\displaystyle TDA\sphericalangle\) egyenesszög, tehát a közös \(\displaystyle D\) csúcsú három szög összege \(\displaystyle 180^{\circ}\), azaz (1) felhasználásával
| \(\displaystyle (2)\) | \(\displaystyle \alpha+\beta+\delta=180^{\circ}.\) |
Elegendő megmutatnunk, hogy \(\displaystyle \delta+\tau=90^{\circ}\), mert ha ez igaz, akkor \(\displaystyle KT\) merőleges \(\displaystyle BS\)-re.
A \(\displaystyle k_2\) körben a \(\displaystyle KA\) és \(\displaystyle KB\) húrok hossza egyenlő, emiatt a hozzájuk tartozó ívek hossza is egyenlő, tehát a kerületi szögek tétele alapján \(\displaystyle KTD\sphericalangle=BTK\sphericalangle=\tau\), ezért \(\displaystyle BTA\sphericalangle=2\tau\). Ez azt jelenti, hogy a \(\displaystyle k_2\) körnek a \(\displaystyle K\) pontot is tartalmazó ívéhez \(\displaystyle 2\tau\) nagyságú kerületi szög tartozik, ebből ugyancsak a kerületi szögek tétele segítségével adódik, hogy
| \(\displaystyle (3)\) | \(\displaystyle BSA\sphericalangle=DSA\sphericalangle=2\tau.\) |
Az \(\displaystyle ADS\) háromszögben a csúcsszögek egyenlősége miatt \(\displaystyle ADS\sphericalangle=\delta\). Az \(\displaystyle AKBS\) négyszög húrnégyszög, amelyben a szemben levő szögek összege \(\displaystyle 180^{\circ}\), ezért
\(\displaystyle \alpha+\beta+SAD\sphericalangle=180^{\circ},\)
ebből (2) szerint
| \(\displaystyle (4)\) | \(\displaystyle SAD\sphericalangle=\delta\) |
következik. Az \(\displaystyle ADS\) háromszögben tehát a szögek összege \(\displaystyle 2\delta+2\tau=180^{\circ}\), vagyis
\(\displaystyle \delta+\tau=90^{\circ},\)
és éppen ezt akartuk igazolni. Tehát \(\displaystyle KT\) valóban merőleges \(\displaystyle BS\)-re.
Megjegyzés. Egyszerűen bizonyítható, hogy a feladat állítása nem csak a feladatban megfogalmazott feltételek mellett teljesül, hanem minden \(\displaystyle k_2\) körön levő \(\displaystyle S\) pont esetén. Különleges eset az, amikor \(\displaystyle S\) azonos \(\displaystyle B\)-vel, ekkor ha a \(\displaystyle BS\) egyenesnek a \(\displaystyle k_2\) kör a \(\displaystyle B\)-beli érintőjét tekintjük, akkor a feladat állítása érvényben marad. Hasonlóan különleges eset az, amikor \(\displaystyle A=S\), ekkor \(\displaystyle A=S=D\) és az \(\displaystyle AD\) egyenes a \(\displaystyle k_1\) kör \(\displaystyle A\) pontbeli érintője lesz, és a feladat állítása így is megmarad, ahogy akkor is, ha \(\displaystyle S=K\). Végül, ha az \(\displaystyle S\) pont és a \(\displaystyle K\)-nak az \(\displaystyle O\)-val átellenes pontja esik egybe, akkor \(\displaystyle BS\) a \(\displaystyle k_1\) kör \(\displaystyle B\)-beli érintője, továbbá \(\displaystyle B=D=T\) és világos, hogy \(\displaystyle KT\) ekkor is merőleges \(\displaystyle BS\)-re.
Statisztika:
87 dolgozat érkezett. 5 pontot kapott: 51 versenyző. 4 pontot kapott: 8 versenyző. 3 pontot kapott: 5 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 1 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 11 dolgozat.
A KöMaL 2025. áprilisi matematika feladatai
