 |
A C. 1859. feladat (2025. május) |
C. 1859. Egy nem szabályos háromszög oldalainak hossza \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\), amelyekre \(\displaystyle {a+b=2c}\) teljesül. Bizonyítsuk be, hogy a háromszög beírt körének középpontját a súlyponttal összekötő szakasz párhuzamos a háromszög valamelyik oldalával.
német versenyfeladat
(5 pont)
A beküldési határidő 2025. június 10-én LEJÁRT.
Megoldás. Azt fogjuk bizonyítani, hogy a háromszög beírt körének \(\displaystyle K\) középpontján és \(\displaystyle S\) súlypontján áthaladó egyenes az \(\displaystyle AB\) oldallal párhuzamos. Legyen a \(\displaystyle K\), illetve \(\displaystyle S\) pontnak az \(\displaystyle AB\) oldalra eső merőleges vetülete \(\displaystyle D\), illetve \(\displaystyle E\), az \(\displaystyle AB\) oldal felezőpontja \(\displaystyle F\), a \(\displaystyle C\) pontból induló magasság talppontja \(\displaystyle G\), továbbá \(\displaystyle KD=r\) valamint \(\displaystyle CG=m\). Tekintsük az alábbi ábrát.
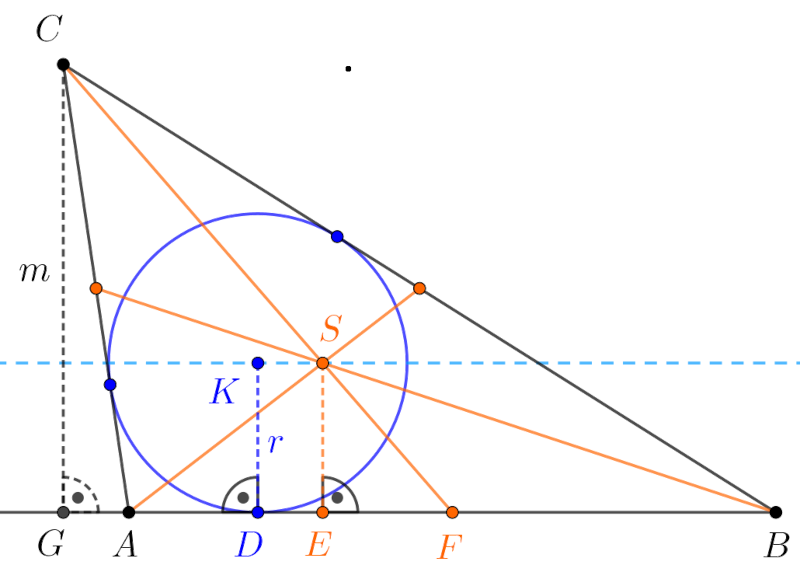
Az \(\displaystyle a+b=2c\) feltételből \(\displaystyle a+b+c=2s=3c\) következik, ahol \(\displaystyle s\) a háromszög félkerülete, ezért \(\displaystyle \displaystyle{s=\frac{3c}{2}}\).
Ismeretes, hogy a háromszög területe kifejezhető a félkerülettel és a beírt kör sugarával \(\displaystyle T=r\cdot s\) alakban, ebből a
| \(\displaystyle (1)\) | \(\displaystyle \displaystyle{T=r\cdot \frac{3c}{2}}\) |
összefüggést kapjuk. A \(\displaystyle T\) terület a \(\displaystyle c\) oldallal és az \(\displaystyle m\) magassággal kifejezve \(\displaystyle \displaystyle{T=\frac{c\cdot m}{2}}\), ez (1)-gyel összevetve azt jelenti, hogy
| \(\displaystyle (2)\) | \(\displaystyle m=3r.\) |
Ugyanakkor az ábrán látható, hogy az \(\displaystyle SEF\) és \(\displaystyle CGF\) háromszögek a megfelelő oldalegyenesek párhuzamossága, illetve egybeesése miatt hasonlók. Mivel az \(\displaystyle S\) súlypont az ismert módon harmadolja a \(\displaystyle CF\) súlyvonalat, ezért a háromszögek hasonlóságának aránya \(\displaystyle \displaystyle{\frac{1}{3}}\), tehát
\(\displaystyle \displaystyle{SE=\frac{m}{3}}.\)
Ebből (2) alapján \(\displaystyle SE=r\) adódik, így az \(\displaystyle S\) pont az \(\displaystyle AB\) oldaltól ugyanolyan távol van, mint a beírt kör \(\displaystyle K\) középpontja, vagyis a \(\displaystyle KS\) egyenes az \(\displaystyle AB\) oldallal valóban párhuzamos.
Megjegyzés. A feladat szövegében nem szerepelt az \(\displaystyle a+b=2c\) feltételnek eleget tevő háromszög létezésének bizonyítása. Könnyen látható azonban, hogy ilyen háromszög létezik, például az \(\displaystyle a=6\); \(\displaystyle b=4\); \(\displaystyle c=5\) oldalakkal rendelkező hegyesszögű, az \(\displaystyle a=3\); \(\displaystyle b=5\); \(\displaystyle c=4\) oldalú derékszögű, vagy az \(\displaystyle a=4\); \(\displaystyle b=9\); \(\displaystyle c=6,5\) oldalú tompaszögű háromszög.
Statisztika:
67 dolgozat érkezett. 5 pontot kapott: Aaishipragya Kahaly, Albert Luca Liliána, Bara Boglárka , Bense Tamás, Bodó Rókus Dániel, Budai Máté, Farkas András, Fülöp Levente, Halász Tamás, Hetyei Dániel, Holló Barnabás, Iván Máté Domonkos, Lovas Márk, Majer Veronika, Máté Kristóf, Mezei Marcell, Molnár Lili, Nelissen Sámuel Zalán, Németh Ábel, Pánovics Máté, Papp Emese Petra, Pázmándi Renáta , Péter Tamás, Poczai Dorottya, Roszik Szabolcs, Szighardt Anna, Szmodics Emese Anna, Yan Zhebeier. 4 pontot kapott: Abonyi Donát Tibor, Kallós Klára, Kámán-Gausz Péter, Kulcsár Anna Zita, Miszori Márton, Molnár-Sáska Tamás, Radošická Emma, Rózsa Zsombor, Serfőző Dávid, Szalóki Árpád, Szathmáry Zalán, Tóth Luca, Winkler-Antal Dalma. 3 pontot kapott: 4 versenyző. 2 pontot kapott: 5 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 5 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 3 dolgozat.
A KöMaL 2025. májusi matematika feladatai
