 |
A C. 1869. feladat (2025. október) |
C. 1869. A \(\displaystyle 20\) méter oldalú \(\displaystyle ABCD\) négyzet \(\displaystyle A\) csúcsából induló fénysugár visszaverődik egymás után a \(\displaystyle BC\), \(\displaystyle CD\), \(\displaystyle DA\) oldalakon és ezután eléri az \(\displaystyle AB\) oldal \(\displaystyle N\) felezőpontját. Mekkora utat tesz meg az \(\displaystyle N\) pontig a fénysugár?
iráni versenyfeladat
(5 pont)
A beküldési határidő 2025. november 10-én LEJÁRT.
Megoldás. Legyenek a fénysugárnak a \(\displaystyle BC\), \(\displaystyle CD\), \(\displaystyle DA\) oldalakkal közös pontjai rendre \(\displaystyle K\), \(\displaystyle L\), \(\displaystyle M\) és legyen \(\displaystyle BK=x\), \(\displaystyle AM=y\), \(\displaystyle CL=z\). A fényvisszaverődés fizikai törvénye szerint a beesési merőlegessel a beeső fénysugár ugyanakkora szöget zár be, mint a visszavert fénysugár (ez a három egyenes egy síkban is van). Legyen ez a szög a \(\displaystyle K, L, M\) beesési pontoknál rendre \(\displaystyle \alpha, \beta, \gamma\).
Tekintsük a következő ábrát, amelyen az egyes pontokban a beesési merőlegeseket szaggatott vonallal jelöltük.
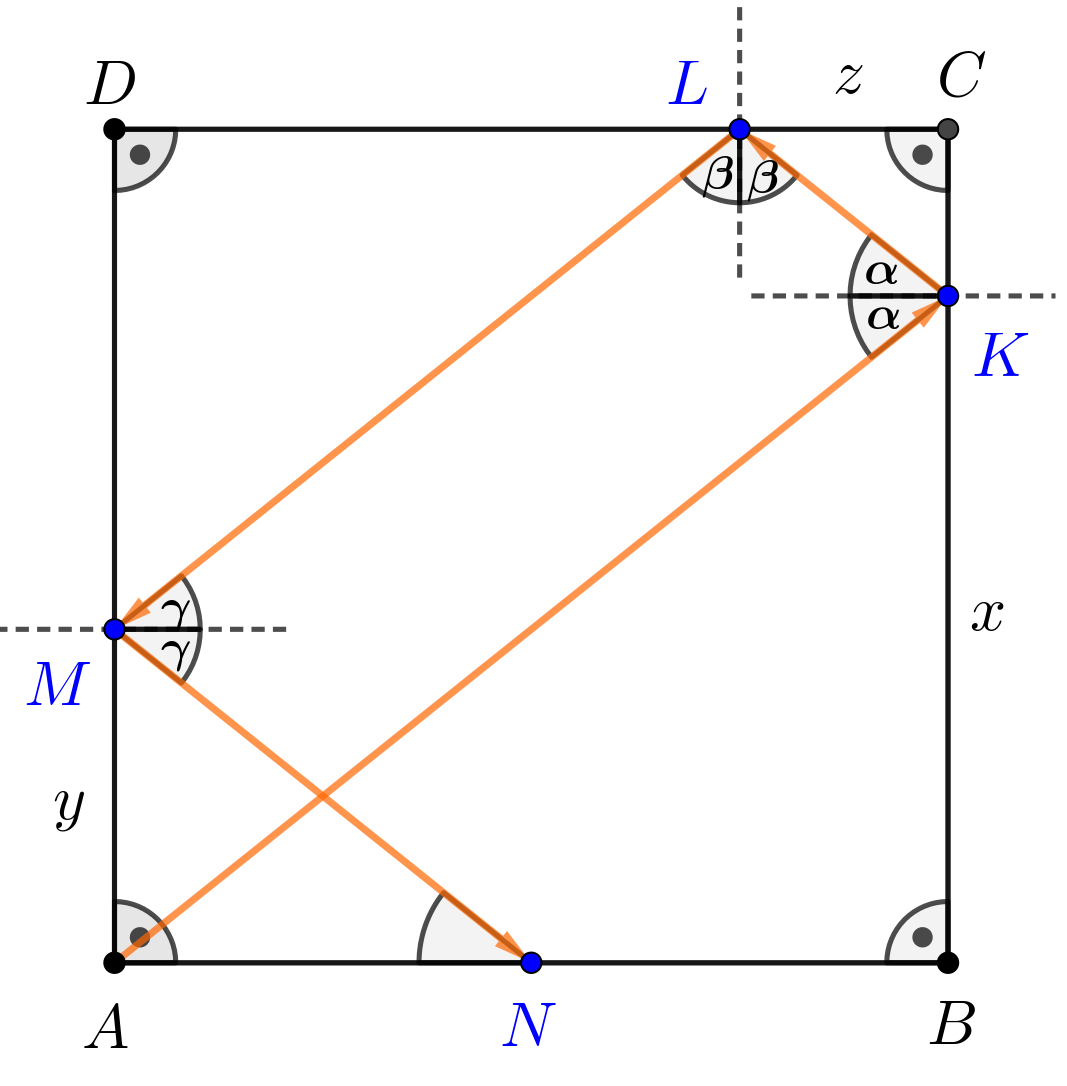
A \(\displaystyle K\), illetve \(\displaystyle L\) pontokban megrajzolt beesési merőlegesek nyilván egymásra is merőlegesek, hiszen \(\displaystyle BC\perp CD\), valamint az \(\displaystyle L\), illetve \(\displaystyle M\) pontokban megrajzolt beesési merőlegesek is merőlegesek egymásra, mert \(\displaystyle CD\perp DA\).
Ebből azonnal következik, hogy a \(\displaystyle K\) és \(\displaystyle M\) pontokban megrajzolt beesési merőlegesek párhuzamosak egymással, tehát \(\displaystyle \alpha=\gamma\), így az \(\displaystyle M\) pontban megrajzolt beesési merőleges és \(\displaystyle AB\) párhuzamossága miatt \(\displaystyle MNA\sphericalangle=\gamma=\alpha\). Az is könnyen látható, hogy \(\displaystyle \alpha+\beta=90^{\circ}\).
A megfelelő szögek egyenlősége miatt az \(\displaystyle ABK\), \(\displaystyle KCL\), \(\displaystyle LDM\) és \(\displaystyle MAN\) derékszögű háromszögek hasonlók, ezért a megfelelő befogók aránya egyenlő:
| \(\displaystyle (1)\) | \(\displaystyle \displaystyle{\frac{x}{20}=\frac{20-x}{z}=\frac{20-y}{20-z}=\frac{y}{10}}.\) |
A felírt törtkifejezések közül az első és utolsó egyenlőségéből
| \(\displaystyle (2)\) | \(\displaystyle x=2y\) |
adódik, az első és a második egyenlőségéből pedig (2) felhasználásával \(\displaystyle \displaystyle{\frac{2y}{20}=\frac{20-2y}{z}}\), ahonnan a műveletek elvégzésével és rendezéssel
| \(\displaystyle (3)\) | \(\displaystyle yz=200-20y.\) |
Az utolsó két tört egyenlősége miatt \(\displaystyle 200-10y=20y-yz\), innen
| \(\displaystyle (4)\) | \(\displaystyle yz=30y-200.\) |
A (3) és (4) egyenletek alapján pedig egyszerű számítással kapjuk, hogy \(\displaystyle y=8\), (2) szerint \(\displaystyle x=16\), végül (3) vagy (4) figyelembe vételével \(\displaystyle z=5\).
Most már kiszámolhatjuk a fénysugár által megtett \(\displaystyle AK+KL+LM+MN\) út hosszát. Az \(\displaystyle ABK\), \(\displaystyle KCL\), \(\displaystyle LDM\), \(\displaystyle MAN\) háromszögekben alkalmazva a Pitagorasz-tételt:
| \(\displaystyle (5)\) | \(\displaystyle AK=\sqrt{656}=4\sqrt{41};\quad KL=\sqrt{41};\quad LM=\sqrt{369}=3\sqrt{41};\quad MN=\sqrt{164}=2\sqrt{41}.\) |
Ezért (5) alapján a fénysugár a négyzetben az \(\displaystyle A\) ponttól az \(\displaystyle N\) pontig \(\displaystyle AK+KL+LM+MN=10\sqrt{41}\) hosszúságegységnyi utat tesz meg.
Statisztika:
226 dolgozat érkezett. 5 pontot kapott: 86 versenyző. 4 pontot kapott: 43 versenyző. 3 pontot kapott: 24 versenyző. 2 pontot kapott: 21 versenyző. 1 pontot kapott: 17 versenyző. 0 pontot kapott: 30 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 2 dolgozat.
A KöMaL 2025. októberi matematika feladatai

