 |
A C. 1871. feladat (2025. október) |
C. 1871. Az \(\displaystyle x^2-6x-4y+9=0\) egyenletű parabola \(\displaystyle F\) fókuszpontján és egy tetszőleges \(\displaystyle P\) pontján átmenő egyenes a parabolát másodszor a \(\displaystyle Q\) pontban metszi. Határozzuk meg a \(\displaystyle PQ\) szakasz felezőpontjai mértani helyének egyenletét.
Javasolta: Bíró Bálint (Eger)
(5 pont)
A beküldési határidő 2025. november 10-én LEJÁRT.
Megoldás. A parabola egyenletét átírhatjuk a \(\displaystyle 4y=x^2-6x+9=(x-3)^2\) alakba, ahonnan
| \(\displaystyle (1)\) | \(\displaystyle \displaystyle{y=\frac{1}{4}\big(x-3\big)^2}.\) |
(1) szerint a parabola tengelye párhuzamos az \(\displaystyle y\)-tengellyel, csúcspontja a \(\displaystyle C(3;0)\) pont, paramétere pedig \(\displaystyle p=2\). Ezekből az is következik, hogy a parabola fókuszpontja \(\displaystyle F(3; 1)\) (vezéregyenese az \(\displaystyle y=-2\) egyenes).
Az \(\displaystyle F\) ponton átmenő egyenesek egyenletét \(\displaystyle y=mx+b\) alakba írhatjuk, ezek átmennek az \(\displaystyle F\) ponton, tehát \(\displaystyle 1=3m+b\) alapján az egyenesek egyenlete
| \(\displaystyle (2)\) | \(\displaystyle y=mx+1-3m.\) |
A feltételek alapján kizárjuk az \(\displaystyle F\) ponton átmenő, az \(\displaystyle y\)-tengellyel párhuzamos egyenest.
Az \(\displaystyle F\) ponton átmenő \(\displaystyle PQ\) egyenes és a parabola közös pontjait az (1)-(2) egyenletrendszer megoldásából kaphatjuk meg. A két egyenlet jobb oldalait egyenlővé téve, a műveletek elvégzése és rendezés után az
\(\displaystyle x^2+(-6-4m)x+5+12m=0\)
másodfokú egyenletet kapjuk. Ennek az egyenletnek biztosan van két valós megoldása, mert a \(\displaystyle PQ\) egyenesnek a feltételek szerint két közös pontja kell legyen a parabolával. A megoldóképlet segítségével:
\(\displaystyle \displaystyle{x_1=3+2m+2\sqrt{m^2+1};\qquad x_2=3+2m-2\sqrt{m^2+1}},\)
ezek tehát a \(\displaystyle P\), illetve \(\displaystyle Q\) pont első koordinátái (ha az \(\displaystyle x_1\) a \(\displaystyle P\) első koordinátája, akkor \(\displaystyle x_2\) a Q ponté és megfordítva). Innen azonnal adódik a \(\displaystyle PQ\) szakasz \(\displaystyle R\) felezőpontjának első koordinátája
| \(\displaystyle (3)\) | \(\displaystyle \displaystyle{x'=\frac{x_1+x_2}{2}=3+2m}.\) |
A \(\displaystyle P\), illetve \(\displaystyle Q\) pont második koordinátáját úgy kapjuk, hogy az \(\displaystyle x_1\) és \(\displaystyle x_2\) koordinátát beírjuk a (2) egyenletbe:
\(\displaystyle \displaystyle{y_1=2m^2+2m\sqrt{m^2+1}+1;\qquad y_2=2m^2-2m\sqrt{m^2+1}+1},\)
innen az \(\displaystyle R\) felezőpont második koordinátája
| \(\displaystyle (4)\) | \(\displaystyle \displaystyle{y'=\frac{y_1+y_2}{2}=2m^2+1}.\) |
A (3) összefüggésből kifejezhetjük \(\displaystyle \displaystyle{m=\frac{x'-3}{2}}\), ezt (4)-be írva
| \(\displaystyle (5)\) | \(\displaystyle \displaystyle{y'=\frac{1}{2}\big(x'-3\big)^2+1}.\) |
Az (5) eredményből láthatóan a \(\displaystyle PQ\) szakasz \(\displaystyle R\) felezőpontjának mértani helye egy parabola, amelynek paramétere \(\displaystyle p'=1\), csúcspontja a \(\displaystyle C'(3;1)\) pont, fókuszpontja \(\displaystyle \displaystyle{F'\Big(3; \frac{3}{2}\Big)}\) (vezéregyenese a \(\displaystyle \displaystyle{y=\frac{1}{2}}\) egyenes).
Megjegyzések.
1) Az \(\displaystyle y'\) értékét úgy is megadható, hogy \(\displaystyle y_1\) és \(\displaystyle y_2\) kiszámítása, majd átlagolása helyett \(\displaystyle x'\) értékét írjuk be a (2) egyenletbe.
2) A két parabola képét megrajzolva a következő ábrát kaphatjuk.
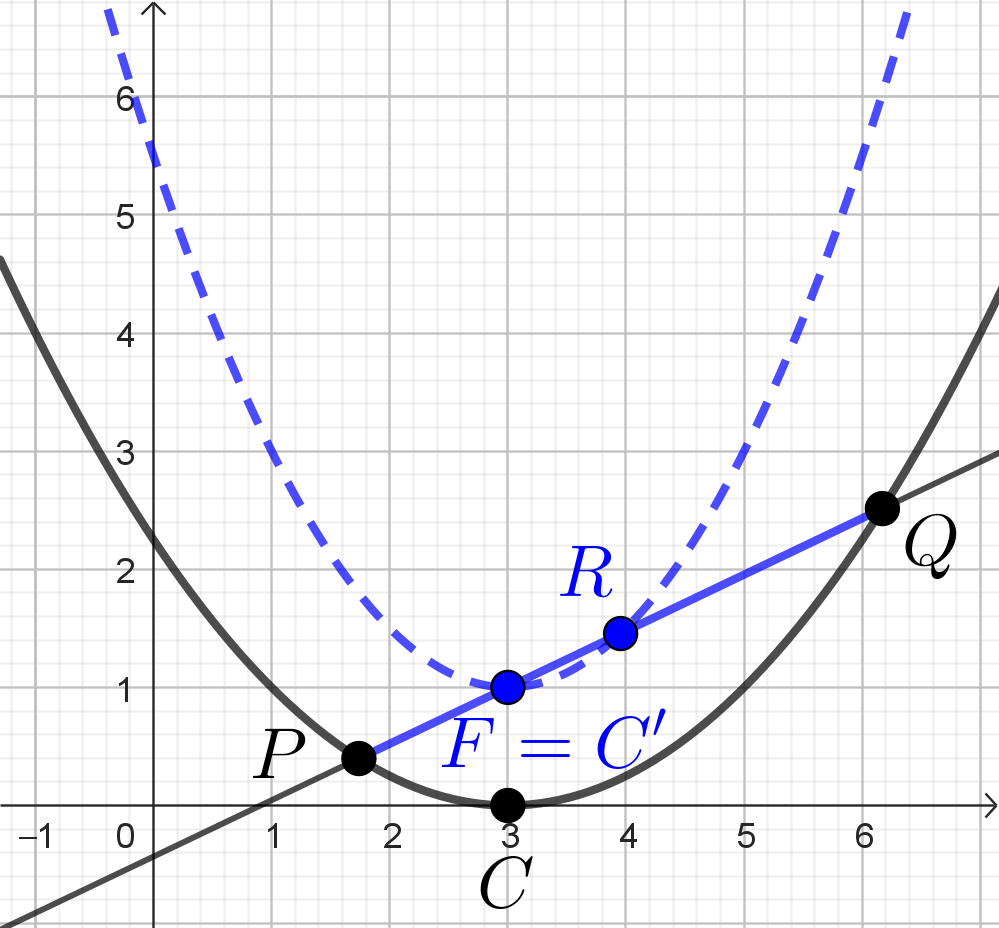
Statisztika:
39 dolgozat érkezett. 5 pontot kapott: Aaishipragya Kahaly, Bán Kincső Panni, Bao Nguyen Gia, Budai Máté, Fülöp Magdaléna, Halmosi Dávid, Hetyei Dániel, Hirmann Dorottya, Kámán-Gausz Péter, Király Zsuzsanna , Németh Ábel, Papp Emese Petra, Poczai Dorottya, Válek Péter, Zádori Gellért. 4 pontot kapott: Abonyi Donát Tibor, Albert Luca Liliána, Forrai Fanni, Miskolczi Máté Pál, Móricz Zsombor, Novák Zétény, Ördög Dominik, Yan Zhebeier. 3 pontot kapott: 8 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 2 versenyző. Nem versenyszerű: 2 dolgozat.
A KöMaL 2025. októberi matematika feladatai

