A C. 979. feladat (2009. február)

C. 979. Piros alapon fehér pöttyös labdánkon harminc (gömbsüveg alakú) pötty található. A labda főkörének kerülete 54 cm, a pöttyök kerülete 11 cm. A labda felszínének hány százaléka pötty?

(5 pont)

A beküldési határidő 2009. március 16-án LEJÁRT.

Megoldás. Jelölje a labdának megfelelő gömb sugarát r, a pöttynek megfelelő gömbsüveg alapkörének sugarát $\varrho$ , magasságát pedig m.

r és $\varrho$ közvetlenül számolható:

$r=\frac{54}{2\pi}\approx8,59;\qquad\qquad\varrho=\frac{11}{2\pi}\approx1,75.$

Messük el a gömböt egy, a középpontján és egy gömbsüveg alapkörének középpontján átmenő síkkal.

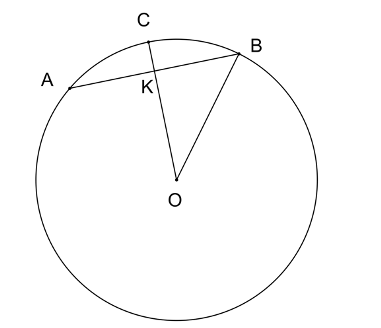
Használjuk az ábra jelöléseit. Ekkor OB=OC=r, KB= $\varrho$ és KC=m. Ebből OK=r-m. Írjuk fel a Pitagorasz-tételt az OKB háromszögre:

r²= $\varrho$ ²+(r-m)²,

amiből

$r-m=\sqrt{r^2-\varrho^2}\approx8,41,$

és így m=r-8,41=0,18.

Egy pötty felszíne:

A_p=2 $\pi$ rm $\approx$ 9,72,

a labda felszíne:

A_l=4 $\pi$ r² $\approx$ 927,25.

A keresett arány: $\frac{30\cdot9,72}{927,25}\approx31,45\%$ .

Statisztika:

254 dolgozat érkezett.

5 pontot kapott: 152 versenyző.

4 pontot kapott: 53 versenyző.

3 pontot kapott: 11 versenyző.

2 pontot kapott: 23 versenyző.

1 pontot kapott: 7 versenyző.

0 pontot kapott: 3 versenyző.

Nem versenyszerű: 5 dolgozat.

A KöMaL 2009. februári matematika feladatai

254 dolgozat érkezett.
5 pontot kapott:	152 versenyző.
4 pontot kapott:	53 versenyző.
3 pontot kapott:	11 versenyző.
2 pontot kapott:	23 versenyző.
1 pontot kapott:	7 versenyző.
0 pontot kapott:	3 versenyző.
Nem versenyszerű:	5 dolgozat.

Már regisztráltál?
Új vendég vagy?