A G. 885. feladat (2025. április)

G. 885. Egy optikai üvegszál magjának törésmutatója \(\displaystyle 1{,}6\), míg a borításáé \(\displaystyle 1{,}5\). Legfeljebb mekkora szöget zárhat be az optikai szál tengelyével egy fénysugár az üvegszálon belül, hogy teljes visszaverődés jöjjön létre a szál belsejében? A tengelyhez képest legfeljebb mekkora szöggel érkezhet a fénysugár levegőből az üvegszál tengelyre merőleges belépési sík közepére?

(3 pont)

A beküldési határidő 2025. május 15-én LEJÁRT.

Megoldás. Teljes visszaverődés az üvegszál magja (angolul core) és borítása (angolul cladding) között jön létre, ahogy ezt az ábra mutatja.

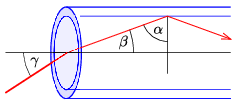
Az \(\displaystyle \alpha\) szög legyen a teljes visszaverődés határszöge, amit így számíthatunk ki:

\(\displaystyle \sin\alpha=\frac{n_2}{n_1}=\frac{1{,}5}{1{,}6}\qquad\Rightarrow\qquad\alpha=69{,}6^\circ\approx 70^\circ,\)

ahol \(\displaystyle n_1\) az üvegszál magjának, \(\displaystyle n_2\) pedig a borításának a törésmutatója. Mivel \(\displaystyle \beta\) éppen \(\displaystyle \alpha\) pótszöge (a derékszögű háromszög két hegyesszögének összege alapján), a fénysugár legfeljebb \(\displaystyle \beta=20^\circ\)-os szöget zárhat be az üvegszál tengelyével.

A \(\displaystyle \gamma\) szöget a Snellius–Descartes-törvény alapján számíthatjuk ki:

\(\displaystyle \frac{\sin\gamma}{\sin\beta}=n_1=1{,}6\qquad\Rightarrow\qquad\gamma=33^\circ.\)

Tehát a tengelyhez képest legfeljebb \(\displaystyle 33^\circ\)-os szöget bezáróan érkezhet a fénysugár az üvegszál belépő lapjának közepére.

Statisztika:

23 dolgozat érkezett.
3 pontot kapott:	Békési Máté, Hegedüs Márk, Horváth Zsombor, József Áron, Kovács Artúr-Lehel, Macskássy Márk, Majer Veronika, Medgyesi András, Molnár Sámuel , Sógor-Jász Soma, Szilaj Petra, Tóth Domonkos, Vízhányó Janka.
2 pontot kapott:	Bora Ádám, Csáki Anikó, Hollósi Dominik, Kovács Tamás , Rácz Koppány Bendeguz.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2025. áprilisi fizika feladatai