A G. 886. feladat (2025. április)

G. 886. Az ábrán látható két egyforma, párhuzamosan kapcsolt síkkondenzátort \(\displaystyle 200~\mathrm{V}\)-ra töltjük, majd lekapcsoljuk a feszültségforrást. Ezután az egyik kondenzátor lemeztávolságát megkétszerezzük, a másikét megfelezzük. (A lemezek között levegő van.)

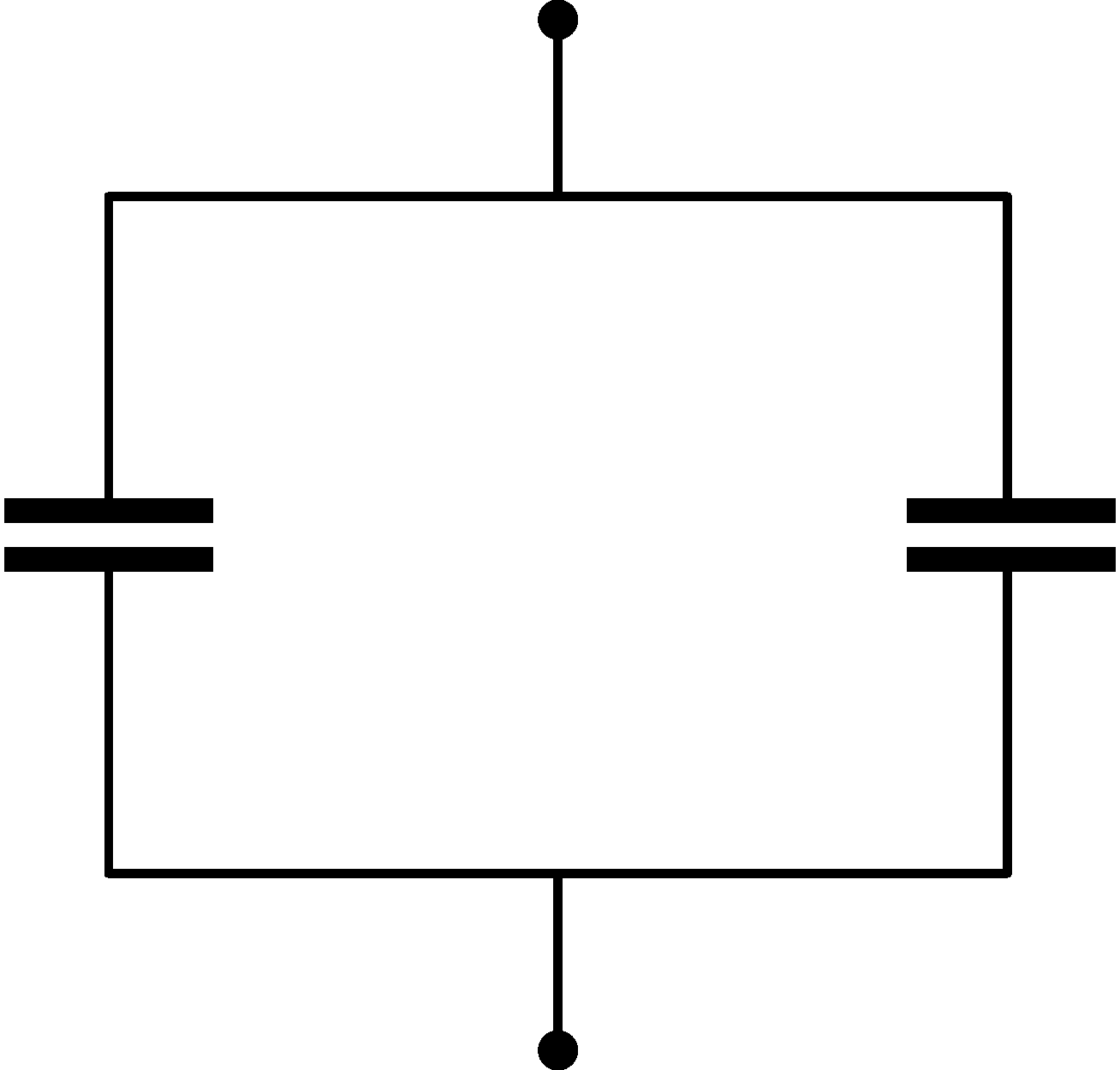
a) Hányszorosára változik az eredő kapacitás?

b) Mekkora lesz a feszültség?

c) Hány százalékkal változik az egyes kondenzátorok elektrosztatikus energiája?

(4 pont)

A beküldési határidő 2025. május 15-én LEJÁRT.

Megoldás. (ÍRTA: HGy) a) Legyen mindkét kondenzátor kapacitása kezdetben \(\displaystyle C\). Mivel a két kondenzátor párhuzamosan van kapcsolva, ezért kezdetben az eredő kapacitás \(\displaystyle C_\mathrm{e}=2C\). A síkkondenzátorokról tudjuk, hogy kapacitásuk így írható fel:

\(\displaystyle C=\varepsilon_0\frac{A}{d},\)

ahol \(\displaystyle A\) a lemezek felülete, \(\displaystyle d\) a közöttük lévő távolság, \(\displaystyle \varepsilon_0\) pedig a vákuum dielektromos állandója. Ha tehát megkétszerezzük a lemezek közötti távolságot, akkor a kondenzátor kapacitása fele akkora lesz: \(\displaystyle \tfrac{C}{2}\). Ha viszont megfelezzük a lemeztávolságot, akkor a kapacitás kétszeresére nő: \(\displaystyle 2C\). Így végül egy \(\displaystyle 2C\) és egy \(\displaystyle \tfrac{C}{2}\) kapacitású kondenzátort kapcsolunk párhuzamosan, így az új eredő kapacitás \(\displaystyle C_\mathrm{e}'=\tfrac{5}{2}C\)-nek adódik. Tehát a kezdeti eredő kapacitás \(\displaystyle \tfrac{5}{4}=1{,}25\)-szörösére növekszik.

b) Kezdetben mindkét kondenzátor feszültsége \(\displaystyle U=200\,\mathrm{V}\), töltésük pedig külön-külön \(\displaystyle Q=CU\) volt. A megoldás kulcsa az, hogy a kezdeti \(\displaystyle 2Q\) töltés megmarad, az egyik kondenzátornak (\(\displaystyle Q+q\))-ra nő a töltése, a másiké (\(\displaystyle Q-q\))-ra csökken. A párhuzamos kapcsolás miatt a két kondenzátor feszültsége megegyezik:

\(\displaystyle U'=\frac{Q+q}{2C}=\frac{Q-q}{C/2} \qquad\Rightarrow\qquad q=\frac{3}{5}Q \qquad\Rightarrow\qquad U'=\frac{Q+\frac{3}{5}Q}{2C}\left(=\frac{Q-\frac{3}{5}Q}{C/2}\right)=\frac{4}{5}\frac{Q}{C}=\frac{4}{5} U=160\,\mathrm{V}.\)

Az eredményt az a) rész eredményéből is megkaphatjuk, hiszen a feszültség az össztöltés és az eredő kapacitás hányadosa:

\(\displaystyle U'=\frac{2Q}{C_\mathrm{e}'}=\frac{4}{5}U=160\,\mathrm{V}.\)

c) Mindkét kondenzátor kezdeti energiája \(\displaystyle \tfrac{1}{2}QU\) alakban írható fel. Az egyik kondenzátor töltése \(\displaystyle \tfrac{8}{5}Q\)-ra növekszik, a másiké \(\displaystyle \tfrac{2}{5}Q\)-ra csökken, míg mindkettő feszültsége \(\displaystyle U'=\tfrac{4}{5}U\)-ra csökken. Így az egyik energiája \(\displaystyle \tfrac{1}{2}\left(\tfrac{8}{5}Q\cdot\tfrac{4}{5}U\right)=\tfrac{16}{25}QU\)-ra növekszik, ami 28%-os növekedés. A másik energiája \(\displaystyle \tfrac{1}{2}\left(\tfrac{2}{5}Q\cdot \tfrac{4}{5}U\right)=\tfrac{4}{25}QU\)-ra csökken, ami 68%-os csökkenés.

Megjegyzés. A teljes rendszer energiája \(\displaystyle QU\)-ról \(\displaystyle \tfrac{16}{25}QU+\tfrac{4}{25}QU=\tfrac{4}{5}QU\)-ra csökken, ami 20%-os csökkenés. Ez egyezésben van azzal, hogy a rendszer össztöltése nem változik, de a feszültsége 20%-kal csökken.

Statisztika:

30 dolgozat érkezett.
4 pontot kapott:	Békési Máté, Csáki Anikó, Hegedüs Márk, Hollósi Dominik, Horváth Zsombor, József Áron, Kakas Noel, Kovács Artúr-Lehel, Kovács Tamás , Lakatos Levente, Majer Veronika, Medgyesi András, Németh Ábel, Patócs 420 Péter, Rácz Koppány Bendeguz, Sipeki Andor, Sógor-Jász Soma, Szighardt Anna, Szilaj Petra, Tóth Domonkos, Vízhányó Janka.
3 pontot kapott:	Csonka Áron, Kossár Benedek Balázs, Molnár Sámuel .
2 pontot kapott:	1 versenyző.
1 pontot kapott:	1 versenyző.

A KöMaL 2025. áprilisi fizika feladatai