A G. 888. feladat (2025. április)

G. 888. Egy vidámparkban egy hatalmas, forgó henger belsejében a henger palástjánál elhelyezett ferde felülethez tapadnak az emberek. A henger sugara \(\displaystyle {R=5~\mathrm{m}}\), a tapadási súrlódási együttható \(\displaystyle {\mu=0{,}25}\), a ferde felület az ábrán látható módon \(\displaystyle {\vartheta=30^{\circ}}\)-os szöget zár be a függőlegessel.

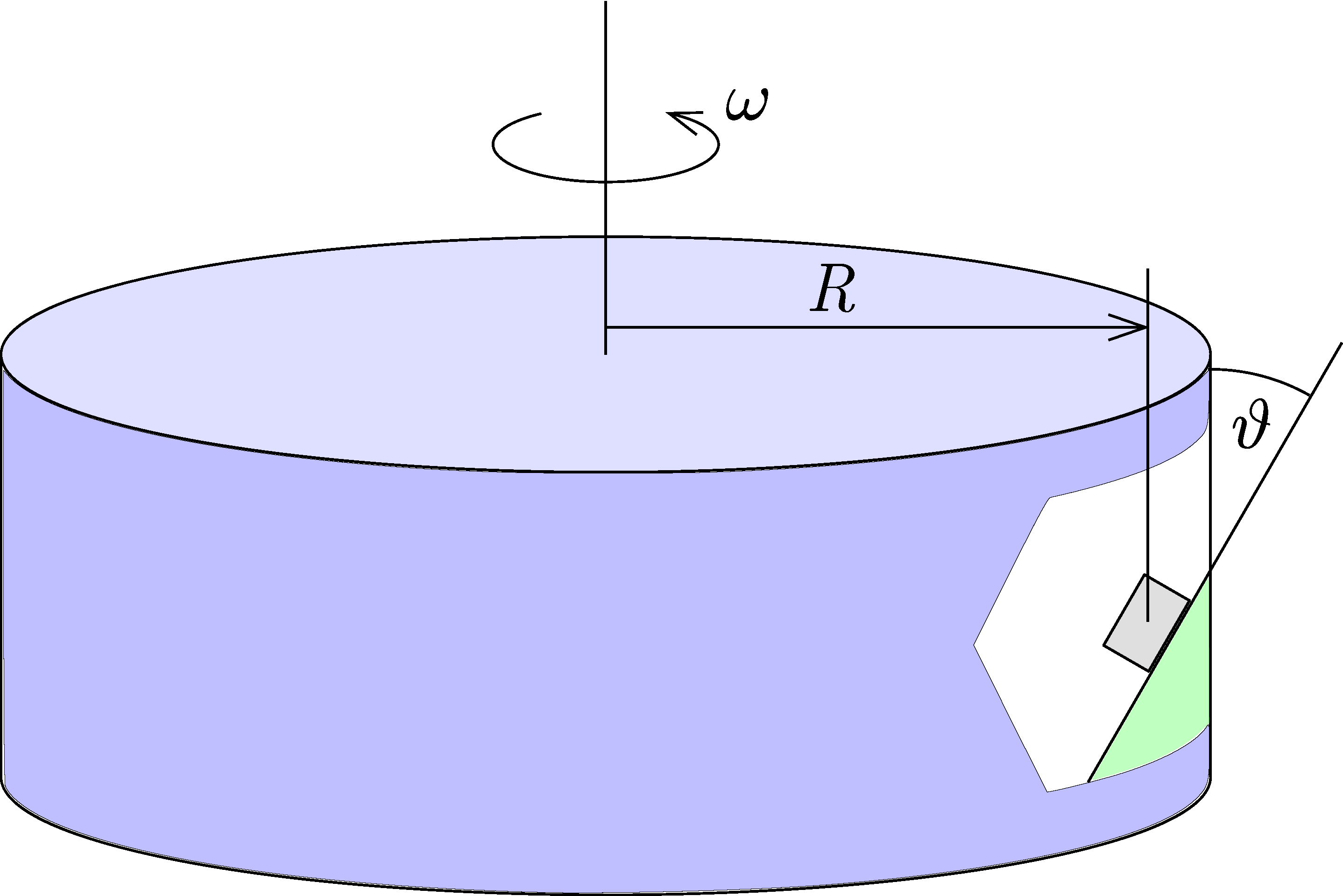
a) Legalább és legfeljebb mennyi lehet a henger szögsebessége, hogy az emberek se lefelé, se felfelé ne csússzanak?

b) Mekkora lehet a súrlódási együttható, hogy akármilyen kicsiny szögsebességnél se csússzanak lefelé az emberek?

c) Mekkora lehet a súrlódási együttható, hogy akármilyen nagy szögsebesség esetén se csússzanak felfelé az emberek?

(4 pont)

A beküldési határidő 2025. május 15-én LEJÁRT.

I. megoldás. a) A hengerrel együtt mozgó rendszerben a ferde felületen lévő testek egyensúlyi állapotban nyugszanak, a rájuk ható erők eredője nulla: \(\displaystyle m\boldsymbol{g}+\boldsymbol{N}+\boldsymbol{S}+\boldsymbol{F}_\mathrm{cf}=0\). Az 1. ábra mutatja az \(\displaystyle mg\) nehézségi erőt, a ferde sík által kifejtett \(\displaystyle N\) nyomóerőt, az \(\displaystyle S=\pm\mu N\) súrlódási erőt és az \(\displaystyle F_\mathrm{cf}=mR\omega^2\) centrifugális erőt. A súrlódási erőben megjelenő \(\displaystyle \pm\) jel arra utal, hogy a számításban a két határesetet tekintjük; a + jelnek az felel meg, amikor a súrlódás még éppen meg tudja akadályozni a test lecsúszását, míg a \(\displaystyle -\) jel esetében a felfelé történő megcsúszást képes még megakadályozni.

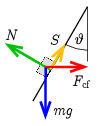
1. ábra

Tekintsük rendre a lejtővel párhuzamos és a lejtőre merőleges összetevők egyensúlyát:

\(\displaystyle mg\cos\vartheta=\pm\mu N+mR\omega^2\sin\vartheta,\)

\(\displaystyle N=mR\omega^2\cos\vartheta+mg\sin\vartheta.\)

A kérdéses szögsebességeket megkapjuk, ha a második egyenletből \(\displaystyle N\)-et beírjuk az elsőbe:

\(\displaystyle \omega=\sqrt{\frac{g(\cos\vartheta\mp\mu\sin\vartheta)}{R(\sin\vartheta\pm\mu\cos\vartheta)}}.\)

Behelyettesítés után azt kapjuk, hogy \(\displaystyle \omega_\mathrm{min}=1{,}42\,\mathrm{s}^{-1}\) (ekkor a számlálóban a \(\displaystyle -\) előjelet, a nevezőben a \(\displaystyle +\) előjelet használtuk), illetve \(\displaystyle \omega_\mathrm{max}=2,62\,\mathrm{s}^{-1}\) (fordított előjelhasználattal).

b) Ha a henger áll, akkor \(\displaystyle \omega=0\), ami azt jelenti, hogy az emberek akkor nem csúsznak le. ha olyan nagy a súrlódás, hogy \(\displaystyle \mu>\frac{1}{\tg\vartheta}=1{,}73.\) (Vigyázat! A függőlegestől mérjük a \(\displaystyle \vartheta\) szöget.)

c) A szögsebesség kifejezésében a nevező nem lehet nulla, sőt negatív sem lehet. Ha formálisan ez jön ki, vagyis \(\displaystyle \mu\geq\tg\vartheta =0{,}577\), akkor a test annyira ráfeszül a ferde síkra, hogy akármilyen nagy \(\displaystyle \omega\) esetén sem csúszik felfelé.

II. megoldás. Egy test akkor nem csúszik meg, ha a nyomóerő és a tapadó súrlódási erő eredője egyensúlyt tud tartani a testre ható többi erő eredőjével. Mivel \(\displaystyle S\leq\mu N\), a két erő eredője legfeljebb

\(\displaystyle \varepsilon=\arctg\frac{S_\mathrm{max}}{N}=\arctg\mu\)

szöget zárhat be a felület normálisával (a felületre merőleges iránnyal). Esetünkben a testre a nyomóerőn és s súrlódási erőn kívül csak a nehézségi erő és a forgó rendszerben fellépő centrifugális erő hat. Mindkét erő arányos a test tömegével, így a két erő eredőjének irányát a függőlegesen lefelé mutató \(\displaystyle g\) és a vízszintesen, sugárirányban kifelé mutató \(\displaystyle a_\mathrm{cf}=\omega^2R\) gyorsulásvektorok \(\displaystyle a\) eredőjének iránya határozza meg.

A feladatunk esetében ez azt jelenti, hogy a két gyorsulásvektor eredője a vízszintessel \(\displaystyle \vartheta-\varepsilon\leq\alpha\leq\vartheta+\varepsilon\) szöget zárhat be (2. ábra).

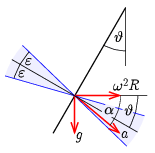
2. ábra

Az ábráról az is látszik, hogy \(\displaystyle \ctg\alpha=\omega^2\tfrac{R}{g}\). Ezután az egyes kérdésekre a válaszok:

a) A súrlódási együttható \(\displaystyle \mu=0{,}25\), ebből \(\displaystyle \varepsilon=\arctg\mu\approx 14^\circ\), \(\displaystyle \vartheta-\varepsilon\approx 16^\circ\), \(\displaystyle \vartheta+\varepsilon\approx 44^\circ\). A szögsebesség-tartományt keressük:

\(\displaystyle \omega=\sqrt{\frac{g}{R}\ctg\alpha},\)

ahol \(\displaystyle \vartheta-\varepsilon\leq\alpha\leq\vartheta+\varepsilon\). A minimális szögsebességhez a maximális \(\displaystyle \alpha\) szög tartozik (és fordítva), így:

b) \(\displaystyle \omega=0\) esetében az eredő gyorsulás függőleges (csak a nehézségi erő hat), így teljesülnie kell a \(\displaystyle \vartheta+\varepsilon\geq 90^\circ\) egyenlőtlenségnek. Ebből \(\displaystyle \varepsilon\geq 60^\circ\) és így \(\displaystyle \mu\geq\tg 60^\circ\approx 1{,}73\) szükséges.

c) Nagyon nagy szögsebesség esetében az eredő gyorsulás közel vízszintes, így a \(\displaystyle \varepsilon\geq\vartheta\) egyenlőtlenségnek kell teljesülnie, amiből \(\displaystyle \varepsilon\geq 30^\circ\) és így \(\displaystyle \mu\geq\tg 30^\circ\approx 0{,}57\) szükséges.

Statisztika:

26 dolgozat érkezett.
4 pontot kapott:	Békési Máté, Csáki Anikó, Hegedüs Márk, Horváth Zsombor, Kossár Benedek Balázs, Kovács Tamás , Lakatos Levente, Macskássy Márk, Molnár Sámuel , Németh Ábel, Patócs 420 Péter, Rácz Koppány Bendeguz, Sipeki Andor, Sógor-Jász Soma, Szabó Tamás.
3 pontot kapott:	Csonka Áron, Vízhányó Janka.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2025. áprilisi fizika feladatai