A G. 900. feladat (2025. október)

G. 900. Megválasztható-e az ábrán látható ohmos ellenállások (nullától különböző) nagysága úgy, hogy az eredő ellenállás az a) és b) esetekben egyenlő legyen?

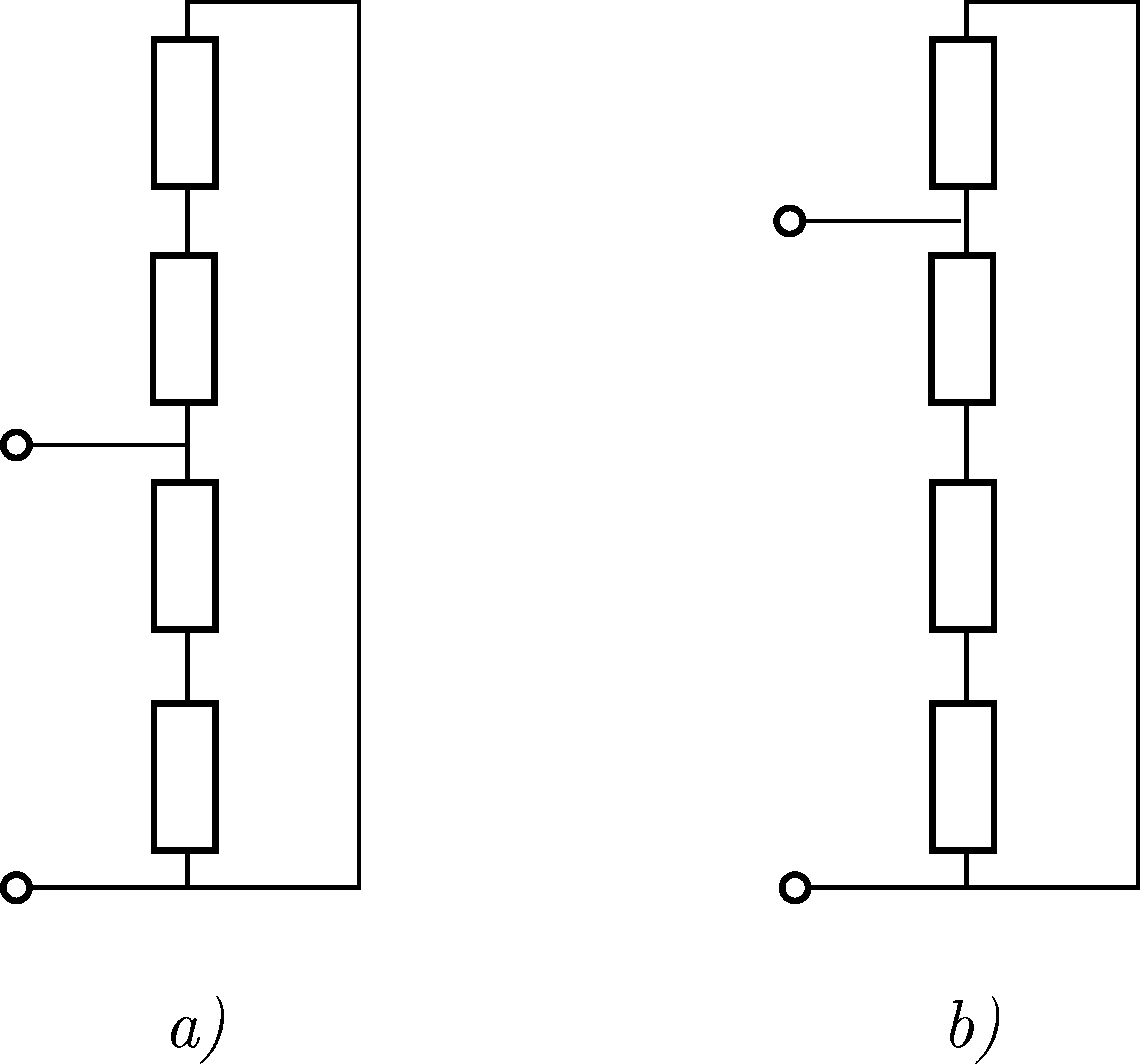
de Châtel Péter (1940–2023) feladata nyomán

(4 pont)

A beküldési határidő 2025. november 17-én LEJÁRT.

Megoldás. Az alsó két ellenállást vonjuk össze egyetlen ellenállásnak, és ezt jelöljük \(\displaystyle R_1\)-gyel. A felette lévő ellenállások legyenek így jelölve: \(\displaystyle R_2\) és \(\displaystyle R_3\). A kapcsolásokat így rajzolhatjuk át:

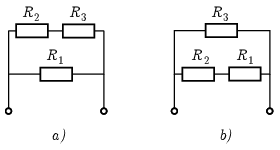
Fejezzük ki, és tegyük egyenlővé a kétféle kapcsolás eredő ellenállását:

\(\displaystyle \frac{R_1(R_2+R_3)}{R_1+R_2+R_3}=\frac{(R_1+R_2)R_3}{R_1+R_2+R_3}\qquad\Rightarrow\qquad R_1R_2+R_1R_3=R_1R_3 +R_2R_3\qquad\Rightarrow\qquad R_1=R_3.\)

Ezzel a feltétellel lényegében az eredeti kapcsolási rajz vízszintes középvonalára tettük szimmetrikussá az összeállítást, tehát nem csoda, hogy az eredő ellenállások megegyeznek. Viszont beláttuk, hogy akkor és csak akkor egyenlő a kétféle eredő ellenállás, ha az alsó két ellenállás összege (\(\displaystyle R_1\)) megegyezik a legfelső ellenállással (\(\displaystyle R_3\)).

Statisztika:

50 dolgozat érkezett.
4 pontot kapott:	Blaskovics Bálint, Horváth 019 Bálint, Majer Veronika, Németh Martin, Olláry Viktor Alex, Steib Miklós, Szighardt Anna, Villant Vanda, Zsilák Márk Péter.
3 pontot kapott:	Bachman Krisztián , Börcsök Péter, Győrffy Réka Rebeka, Hollósi Dominik, Horváth Péter, Kakas Noel, Kelepecz Kornél Zoltán, Kovács Artúr-Lehel, Lukács Kristóf Pál, Rácz Koppány Bendeguz, Sógor-Jász Soma, Sőtér Hunor Marcell, Sőtér Jázmin Sára, Szabó-Medve Boldizsár, Tóth Domonkos, Vincze Blanka Anna.
2 pontot kapott:	12 versenyző.
1 pontot kapott:	5 versenyző.
0 pontot kapott:	4 versenyző.

A KöMaL 2025. októberi fizika feladatai