Az I. 673. feladat (2025. október)

I. 673. Figyelem! A nyomtatott lapban hibásan I. 674. sorszámmal jelent meg ez a feladat!

Ez a feladat az előző tanévben elkezdett prímekkel kapcsolatos sorozat (I. 633., I. 641. és I. 661.) negyedik része.

Additív prímeknek nevezzük az olyan prímszámok, amelyek számjegyei összege is prím. Például az \(\displaystyle 541\,579\) additív prím, hiszen prím, és számjegyeinek összege 31, ami szintén prím.

Bölcsföldi–Dömötör-prímek a (tízes számrendszerben) azon prímszámok, amelyek minden számjegye prím (\(\displaystyle 2\), \(\displaystyle 3\), \(\displaystyle 5\) vagy \(\displaystyle 7\)), a számjegyek száma és összege is prím. Például a \(\displaystyle 33\,223\) prímszám, számjegyeinek száma 5 és összegük 13.

Szimmetrikus prímeknek (a tízes számrendszerben) azokat a prímszámokat nevezzük, amelyek minden számjegye prím, számjegyeinek száma és számjegyeinek összege is prím, továbbá a szám középpontosan szimmetrikus a középső számjegyre. Például a \(\displaystyle 35\,753\) prím, minden számjegye prím, számjegyeinek száma 5, azok összege 23, ezek is prímek és középpontosan szimmetrikus a középső számjegyre.

Háromrészes prímek a (tízes számrendszerben) azok a prímszámok, amelyeknél a számjegyek száma \(\displaystyle 3k\), ahol \(\displaystyle k\geq 1\) egész, és három egyenlő hosszú részre osztva a számot, mindegyik rész is prím. Például a \(\displaystyle 295\,319\) prímszám háromrészes prím, hiszen hatjegyű és részei: 29, 53 és 19 is prímek.

Négyrészes prímek a (tízes számrendszerben) azok a prímszámok, amelyeknél a számjegyek száma \(\displaystyle 4k\), ahol \(\displaystyle k\geq 1\) egész, és négy egyenlő hosszú részre osztva a számot, mindegyik rész is prím. Például a 2557 prímszám négyrészes prím, hiszen négyjegyű, és részei: 2, 5, 5 és 7 is prímek.

1. Készítsünk egy táblázatkezelő munkafüzetben primek néven munkalapot és munkánkat mentsük primek_megint néven a táblázatkezelő program alapértelmezett formátumában.
2. Illesszük be az A3 cellától az \(\displaystyle 1\,000\,000\)-nál nem nagyobb prímek listáját a primek1000000ig.txt fájlból. Az első két sorba oszlopfeliratokat készíthetünk a számításokhoz.
3. Válogassuk ki az öt prímcsoport \(\displaystyle 1\,000\,000\) alatti prímek közé eső tagjait. A számításokat ezen a munkalapon végezzük.
4. Hozzunk létre egy eredmények nevű munkalapot, amelynek A oszlopát töltsük fel 1-től egész számokkal addig, amennyi a speciális prímszámok darabszámának maximuma. A következő oszlopokban határozzuk meg, minden prímszámtípusnál helykihagyás nélkül, növekvő sorrendben:
1. A B oszlopban az additív prímeket.
2. A C oszlopban a Bölcsföldi–Dömötör-prímeket.
3. A D oszlopban a szimmetrikus prímeket.
4. Az E oszlopban a talált háromrészes prímeket.
5. Végezetül az F oszlopba pedig a négyrészes prímek kerüljenek.
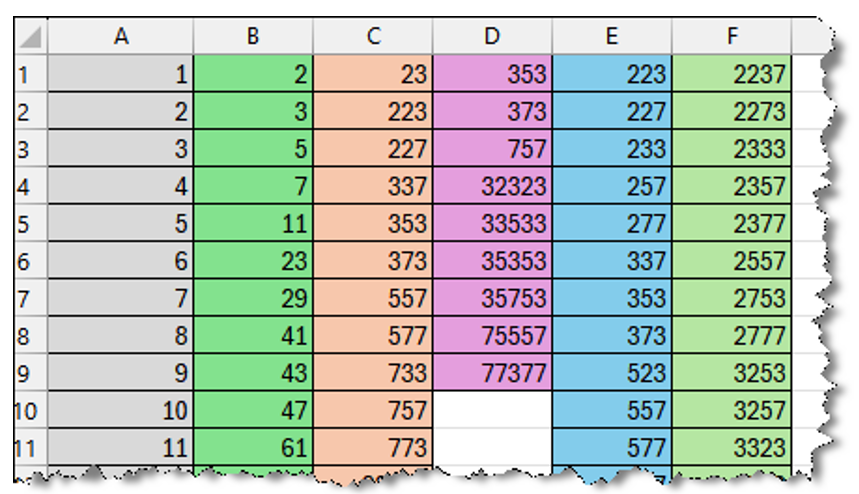
5. A munkalap adattartományát formázzuk a minta szerint!



6. Készítsük el az eredmények munkalapon az adott helyre a mintán látható táblázatot.



7. Számítsuk ki és jelenítsük meg a hiányzó adatokat.
8. Mindkét munkalapon cseréljük le oszloponként az első 99 sor utáni képleteket az értékükre.

Segédszámításokat a primek munkalapon végezhetünk. A megoldásban saját függvény vagy makró nem használható.

Beküldendő az i673.zip tömörtett állományban a munkafüzet az eredeti nevén xlsb formátumban (bináris munkafüzetként) és egy rövid dokumentáció, amelyben szerepel a kiválogatások módszere, a táblázatkezelő neve, verziószáma.

Letölthető fájl: primek1000000ig.txt

(10 pont)

A beküldési határidő 2025. november 17-én LEJÁRT.

Szekeres Linda mintaszerű megoldása: primekmegint.xlsb

magyarazat.txt

Statisztika:

9 dolgozat érkezett.
10 pontot kapott:	Bortnyik Zétény, Rajtik Sándor Barnabás, Szabó Imre Bence, Szekeres Linda.
5 pontot kapott:	1 versenyző.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	1 versenyző.

A KöMaL 2025. októberi informatika feladatai