Az I. 674. feladat (2025. október)

I. 674. Figyelem! A nyomtatott lapban hibásan I. 675. sorszámmal jelent meg ez a feladat!

Egy falrészlet azonos méretű, de különböző tömegű téglákból épült fel az alábbi ábrának megfelelően. Az alsó sorban lévő téglák a földön fekszenek szorosan egymás mellett. A fölöttük lévő téglák az alatta lévő téglákon fekszenek, azokhoz képest egyharmad téglaszélességgel elcsúsztatva jobbra.

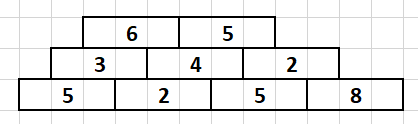
A téglákon lévő számok az adott tégla tömegét mutatják. A legalsó sorban \(\displaystyle N\) darab tégla fekszik, a többi sor mindegyikében eggyel kevesebb, mint az alatta lévőben. Összesen \(\displaystyle K\) sorból áll a falrészlet. A fenti ábra esetén \(\displaystyle N=4\) és \(\displaystyle K=3\).

A téglák közül bármelyik kiemelhető és áthelyezhető, de három szabályt be kell tartani:

1. kiemeléskor az üresen maradt hely miatt a falrészlet nem omolhat le, tehát egyetlen másik tégla sem eshet vagy billenhet le;
2. áthelyezés után is egy egybefüggő falrészlet kell létrejöjjön, tehát a téglák továbbra is egymáshoz illeszkednek (a kiemelt tégla helyét leszámítva), a korábbi egyharmad téglaszélességgel elcsúsztatva;
3. az áthelyezett téglát olyan módon kell elhelyezni, hogy az biztosan feküdjön vagy a földön, vagy az alatta lévő sor tégláján úgy, hogy ne billenjen le.

A fenti ábrán a felső sor bármelyik téglája kivehető és áthelyezhető például a többi sor jobb oldali végére vagy a felső sor fölé egy új sorként, ahol nem billen el. Hasonló módon kiemelhető minden sor utolsó téglája.

Az építész szeretné átrendezni a téglákat úgy, hogy ne forduljon elő, hogy nehezebb tégla fekszik egy vagy két másik, könnyebb téglán. Ehhez a fenti szabályok szerint áthelyezhet téglákat, de a végén vissza szeretné kapni a téglák eredeti elrendezését az eredeti helyen.

Készítsünk programot i674 néven, amely javaslatot tesz a téglák szabályok szerinti áthelyezésére, hogy azok az építész kívánságának megfelelően helyezkedjenek el. Több megoldás lehetséges, elég egyet megadni, de törekedjünk a kevesebb áthelyezéssel járó megoldásra. A megoldások értékelése során az áthelyezések számát is figyelembe vesszük.

A program standard bemenetének első sorában az alsó sorban lévő téglák \(\displaystyle N\) száma (\(\displaystyle 3\leq N\leq 10\)) és a falrészlet magasságának \(\displaystyle K\) száma (\(\displaystyle 3\leq K\leq N\)) szerepel. A következő sorban egy-egy kettőskereszt `#' jellel elválasztva a falrészlet soraiban lévő téglák tömege szerepel. A téglák számai és a `#' jelek között egy szóköz az elválasztó.

A program a standard kimenet első sorába írja ki az áthelyezések \(\displaystyle Z\) számát, majd a következő sorokban az egyes áthelyezések utáni állapotát a falrészletnek. A \(\displaystyle Z\) számú sorba a bemenethez hasonlóan írjuk ki a falrészlet soraiban lévő téglák tömegét. A fal sorait `#' jellel válasszuk el, a `#' jel valamint a számok között egy-egy szóköz legyen, a bemenethez hasonlóan. Amennyiben a sor valamely részén üres hely van, azt a nulla számmal jelezzük.

Példa:

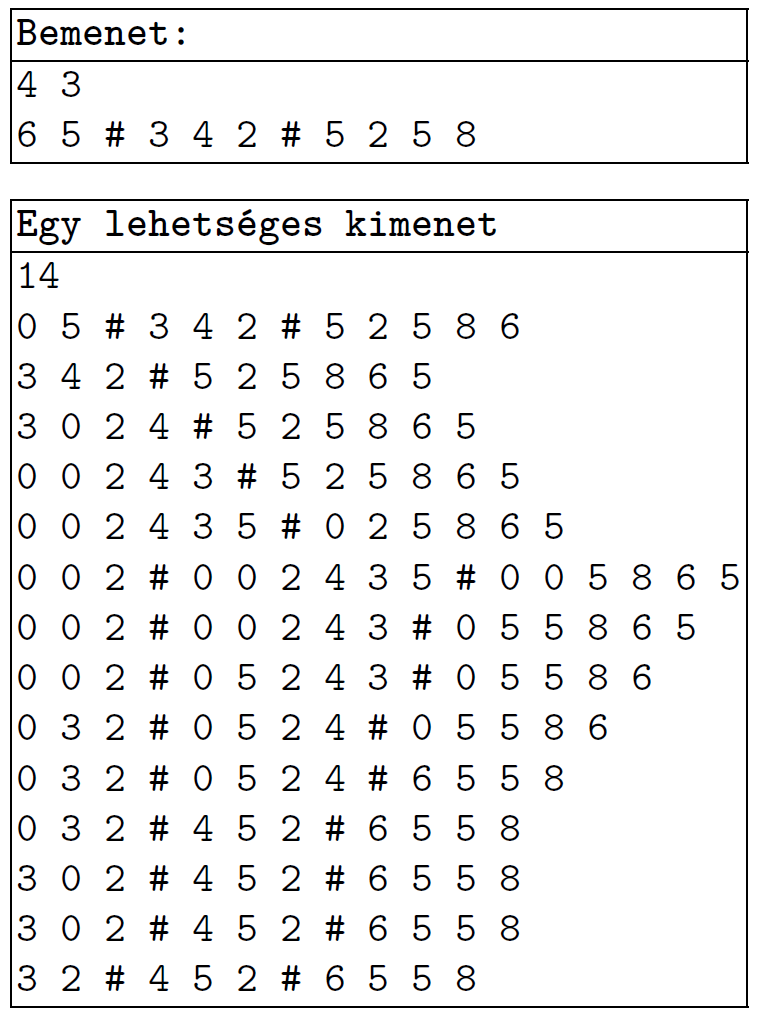
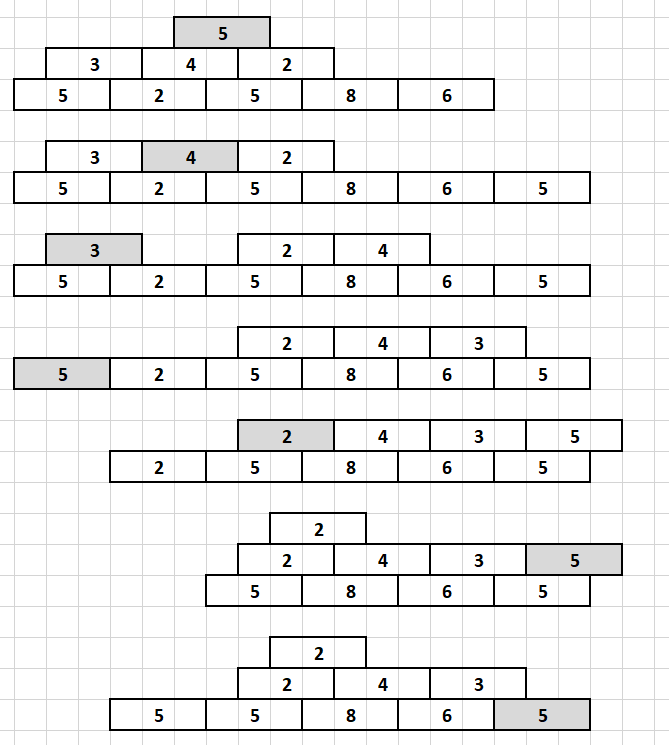
A példához tartozó ábra nem teljes, csak az első 7 áthelyezés utáni állapotot tartalmazza. A következő lépésben áthelyezendő téglát minden esetben szürkével jelöltük.

Beküldendő egy tömörített i674.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.

(10 pont)

A beküldési határidő 2025. november 17-én LEJÁRT.

Statisztika:

Az I. 674. feladat értékelése még nem fejeződött be.

A KöMaL 2025. októberi informatika feladatai