Problem K/C. 822. (September 2024)

K/C. 822. Kati has to calculate the area of the cyclic pentagon in the diagram. The lengths of the sides measured in cm are given in the diagram. Kati obtained the result \(\displaystyle 30+10{,}5\sqrt{30}~\textrm{cm}^2\). Has she calculated correctly?

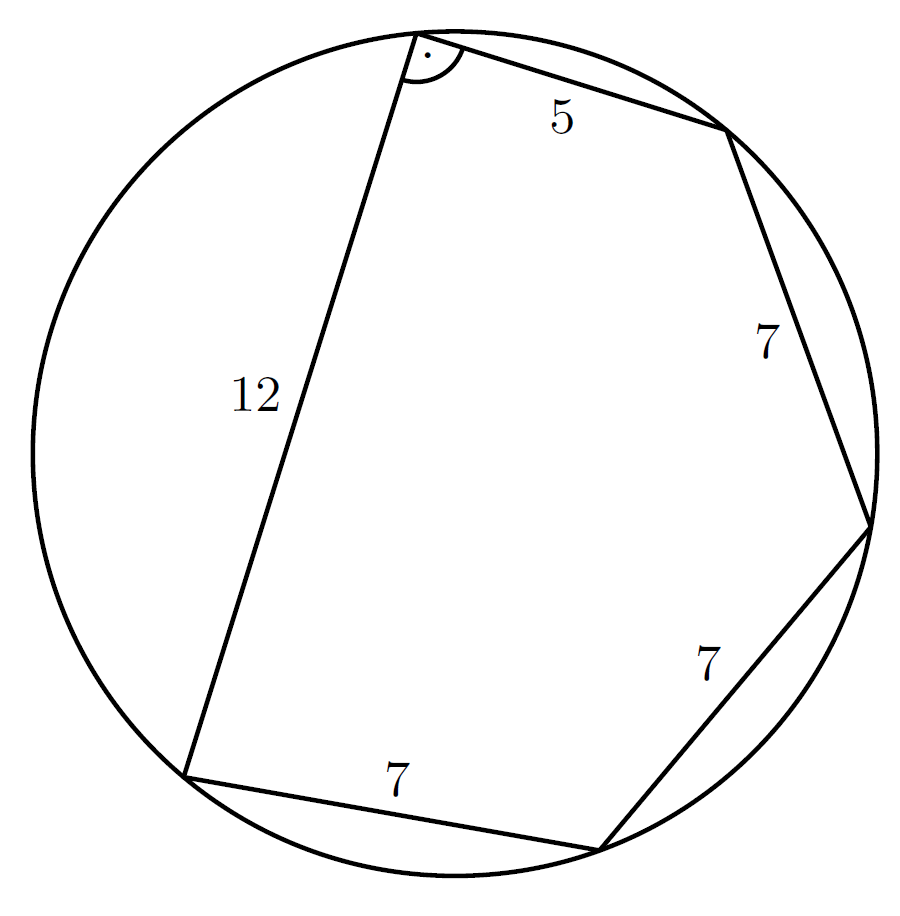
(5 pont)

Deadline expired on October 10, 2024.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Kati nem számolhatott jól, ugyanis a feladatban szereplő adatokkal rendelkező ötszög nem létezik.

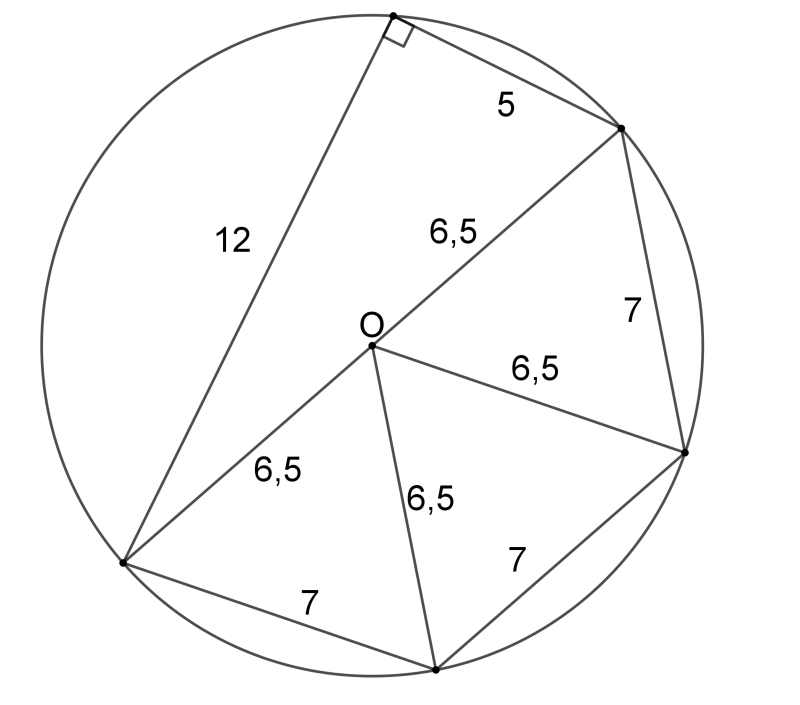
Az \(\displaystyle AC\) a \(\displaystyle B\)-nél levő derékszög miatt 13 cm hosszú, és a Thalész-tétel megfordítása miatt egyben a kör átmérője. A kör sugara így 6,5 cm. Az \(\displaystyle OCD\), \(\displaystyle ODE\) és \(\displaystyle OEA\) háromszögek egybevágók, ezért az \(\displaystyle O\)-nál levő szögük 60 fokos, ekkor viszont, mivel egyenlő szárúak, szabályos háromszögek. Így a 7 cm hosszúnak jelölt oldalak hossza csak 6,5 cm lehetne, tehát az ábrán látható \(\displaystyle AEDCB\) ötszög ezekkel az adatokkal nem létezik.

Statistics:

307 students sent a solution.
5 points:	Araguas Mátyás, Bara Boglárka , Barta Zsófia, Bloemsma Péter Sándor, Bodó Rókus Dániel, Chen Zhibo, Csáti Ambrus, Dornbach Bernadett, Farkas Noémi , Fehér Ádám, Feith Benedek, Halász Tamás, Kapiller Ákos Péter, Kerekes 333 Zoltán, Kolencsik Nándor, Kóródy Vera, Kothencz Luca, Kovács 444 Kamilla, Kovács Dorka Sára, Kudomrák Lili Anna , Kun Milán, Kun Petra, Li Mingdao, Márfai Lili, Maróti Olga, Mateas Isabelle, Molnár Levente, Patócs 420 Péter, Pázmándi Renáta , Péter Tamás, Piller Zsófia, Pivárcsik Márk, Pocsay Bence Máté, Poczai Dorottya, Radošická Emma, Rózsa Péter, Sajó Marcell 16, Szabados Ákos, Szabó Máté, Szalóki Árpád, Szathmáry Zalán, Szedmák Szabrina, Szélpál Botond, Szighardt Anna, Tófalvy Máté, Tóth Luca, Válek Péter, Viczián Adél.
4 points:	16 students.
3 points:	33 students.
2 points:	41 students.
1 point:	91 students.
0 point:	17 students.
Unfair, not evaluated:	7 solutionss.
Not shown because of missing birth date or parental permission:	46 solutions.

Problems in Mathematics of KöMaL, September 2024